(13分)三棱锥P-ABC中,三条棱PC.AC.BC两两垂直,长都等于2,M为PA的中点,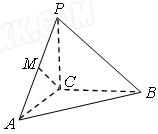
(1)求异面直线CM与AB所成角θ的余弦值;
(2)过点M作一个与平面ABC平行的平面
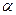 ,将此三棱锥截成两部分,分别求这两部分的体积
,将此三棱锥截成两部分,分别求这两部分的体积
已知椭圆 的中心为坐标原点,其离心率为
的中心为坐标原点,其离心率为 ,椭圆
,椭圆 的一个焦点和抛物线
的一个焦点和抛物线 的焦点重合。
的焦点重合。
(1)求椭圆 的方程
的方程
(2)过点 的动直线
的动直线 交椭圆
交椭圆 于
于 、
、 两点,试问:在坐标平面上是否存
两点,试问:在坐标平面上是否存在一个定点 ,使得无论
,使得无论 如何转动,以
如何转动,以 为直径的圆恒过点
为直径的圆恒过点 ,若存在,说出点
,若存在,说出点 的坐标,若不存在,说明理由。
的坐标,若不存在,说明理由。
已知抛物线

 ,过其焦点且斜率为-1的直线交抛物线于
,过其焦点且斜率为-1的直线交抛物线于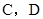 两点,若线段
两点,若线段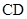 的中点的纵坐标为-2
的中点的纵坐标为-2
(1)求抛物线 的方程;
的方程;
(2)过点 的直线交抛物线
的直线交抛物线 于
于 两不同点,交
两不同点,交 轴于点
轴于点 ,已知
,已知 ,则
,则 是否为定值?若是,求出其值;若不是,说明理由.
是否为定值?若是,求出其值;若不是,说明理由.
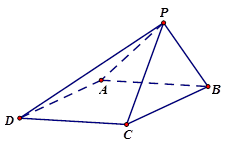
如图,已知四棱锥 的底面为菱形,
的底面为菱形, ,
,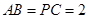 ,
,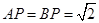 .
.
(1)求证: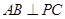 ;
;
(2)求二面角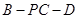 的余弦值.
的余弦值.
一个盒子里装有三张卡片,分别标记有数字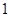 ,
, ,
,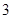 ,这三张卡片除标记的数字外完全相同。随机有放回地抽取
,这三张卡片除标记的数字外完全相同。随机有放回地抽取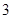 次,每次抽取
次,每次抽取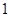 张,将抽取的卡片上的数字依次记为
张,将抽取的卡片上的数字依次记为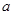 ,
,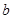 ,
,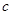 .
.
(1)求“抽取的卡片上的数字满足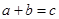 ”的概率;
”的概率;
(2)求“抽取的卡片上的数字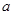 ,
,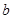 ,
,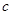 不完全相同”的概率.
不完全相同”的概率.
已知空间中三点A(-2,0,2),B(-1,1,2),C(-3,0,4),设a= ,b=
,b=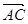 .
.
(1)求向量a与向量b的夹角的余弦值;
(2)若ka+b与ka-2b互相垂直,求实数k的值