某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数: ,其中
,其中 是仪器的月产量.
是仪器的月产量.
(1)将利润 表示为月产量
表示为月产量 的函数
的函数
(2)当月产量 为何值时,公司所获利润最大?最大利润是多少元?(总收益=总成本+利润)
为何值时,公司所获利润最大?最大利润是多少元?(总收益=总成本+利润)
已知点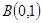 ,点
,点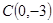 ,直线
,直线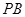 、
、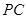 都是圆
都是圆 的切线(
的切线(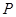 点不在
点不在 轴上)。
轴上)。
⑴求过点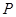 且焦点在
且焦点在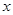 轴上抛物线的标准方程;
轴上抛物线的标准方程;
⑵过点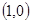 作直线
作直线 与⑴中的抛物线相交于
与⑴中的抛物线相交于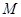 、
、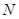 两点,问是否存在定点
两点,问是否存在定点 ,使
,使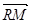 .
. 为常数?若存在,求出点
为常数?若存在,求出点 的坐标与常数;若不存在,请说明理由。
的坐标与常数;若不存在,请说明理由。
一学生参加某高校的自主招生考试,须依次参加A、B、C、D、E五项考试,如果前四项中有两项不合格或第五项不合格,则该考生就被淘汰,考试即结束;考生未被淘汰时,一定继续参加后面的考试。已知每一项测试都是相互独立的,该生参加A、B、C、D四项考试不合格的概率均为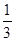 ,参加第五项不合格的概率为
,参加第五项不合格的概率为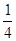 。
。
⑴求该生被录取的概率;
⑵记该生参加考试的项数为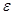 ,求
,求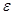 的分布列和期望。
的分布列和期望。
一个多面体的直观图和三视图如图所示,其中 、
、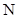 分别是
分别是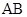 、
、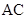 的中点,
的中点,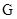 是
是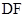 上的一动点,主视图与俯视图都为正方形。
上的一动点,主视图与俯视图都为正方形。

⑴求证: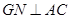 ;
;
⑵当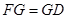 时,在棱
时,在棱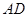 上确定一点
上确定一点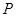 ,使得
,使得 ∥平面
∥平面 ,并给出证明。
,并给出证明。
⑶求二面角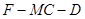 的平面角余弦值。
的平面角余弦值。
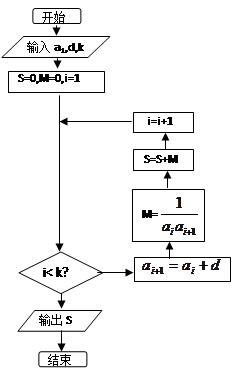
已知数列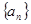 的各项全为正数,观察流程图,当
的各项全为正数,观察流程图,当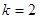 时,
时, ;当
;当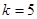 时,
时, ;
;
⑴写出 时,
时, 的表达式(用,
的表达式(用,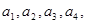 等表示);
等表示);
⑵求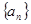 的通项公式;
的通项公式;
⑶令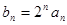 ,求
,求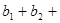
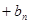 .
.
(本小题满分14分)已知函数 ,其中
,其中
(Ⅰ)求 在
在 上的单调区间;
上的单调区间;
(Ⅱ)求 在
在 (
( 为自然对数的底数)上的最大值;
为自然对数的底数)上的最大值;
(III)对任意给定的正实数 ,曲线
,曲线 上是否存在两点
上是否存在两点 、
、 ,使得
,使得 是以原点
是以原点 为直角顶点的直角三角形,且此三角形斜边中点在
为直角顶点的直角三角形,且此三角形斜边中点在 轴上?
轴上?