人和雪橇的总质量为75kg，沿倾角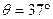且足够长的斜坡向下运动，已-优题课

题文

人和雪橇的总质量为75kg，沿倾角且足够长的斜坡向下运动，已知雪橇所受的空气阻力与速度成正比，比例系数k未知，从某时刻开始计时，测得雪橇运动的v-t图象如图中的曲线AD所示，图中AB是曲线在A点的切线，切线上一点B的坐标为（4，15），CD是曲线AD的渐近线，g取10m/s²，试回答和求解：
（1）雪橇在下滑过程中，开始做什么运动，最后做什么运动？
（2）当雪橇的速度为5m/s时，雪橇的加速度为多大？
（3）雪橇与斜坡间的动摩擦因数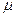多大？

科目物理题型计算题难度较难

登录免费查看答案和解析

相关试题

运动的原子核 ${}_{Z}^{A}X$ 放出 $α$ 粒子后变成静止的原子核 $Y$ 。已知 $X$ 、 $Y$ 和 $α$ 粒子的质量分别是 $M$ 、 $m_{1}$ 和 $m_{2}$ ，真空中的光速为 $c$ ， $α$ 粒子的速度远小于光速。求反应后与反应前的总动能之差以及 $α$ 粒子的动能。

氢原子基态的能量为 $E_{1} = - 13.6 e V$ 。大量氢原子处于某一激发态。由这些氢原子可能发出的所有光子中，频率最大的光子能量为0.96 $E_{1}$ ，频率最小的光子的能量为 $e V$ （保留2位有效数字），这些光子可具有种不同的频率。

一半径为 $R$ 的半圆形玻璃砖，横截面如图所示。已知玻璃的全反射临界角 $r （ r < \frac{π}{3})$ 。与玻璃砖的底平面成（ $\frac{π}{2} - r$ ）角度、且与玻璃砖横截面平行的平行光射到玻璃砖的半圆柱面上。经柱面折射后，有部分光（包括与柱面相切的入射光）能直接从玻璃砖底面射出。若忽略经半圆柱内表面反射后射出的光，求底面透光部分的宽度（）。

如图所示，一底面积为 $S$ 、内壁光滑的圆柱形容器竖直放置在水平地面上，开口向上，内有两个质量均为 $m$ 的相同活塞 $A$ 和 $B$ ；在 $A$ 与 $B$ 之间、 $B$ 与容器底面之间分别封有一定量的同样的理想气体，平衡时体积均为 $V$ 。已知容器内气体温度始终不变，重力加速度大小为 $g$ ，外界大气压强为 $P_{O}$ 。现假设活塞 $B$ 发生缓慢漏气，致使 $B$ 最终与容器底面接触。求活塞 $A$ 移动的距离。

已知地球大气层的厚度 $h$ 远小于地球半径 $R$ ，空气平均摩尔质量为 $M$ ，阿伏伽德罗常数为，地面大气压强为，重力加速度大小为 $g$ 。由此可以估算得，地球大气层空气分子总数为，空气分子之间的平均距离为。

试卷网试题网古诗词网作文网范文网