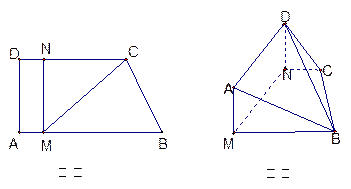
(本小题满分13分)如图甲,直角梯形 中,
中,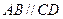 ,
,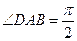 ,点
,点 、
、 分别在
分别在 ,
, 上,且
上,且 ,
,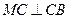 ,
,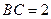 ,
, ,现将梯形
,现将梯形 沿
沿 折起,使平面
折起,使平面 与平面
与平面 垂直(如图乙).
垂直(如图乙).
(Ⅰ)求证: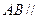 平面
平面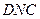 ;
;
(Ⅱ)当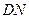 的长为何值时,
的长为何值时,
二面角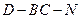 的大小为
的大小为 ?
?
.(本小题满分13分)
已知函数f(x)=sinωx·cosωx-cos2ωx(ω>0)的最小正周期为.
(Ⅰ)求ω的值;
(Ⅱ)设△ABC的三边a、b、c满足b2=ac,且边b所对的角为x,求此时f(x)的值域.
(本小题满分14分)
已 知直线
知直线 :
: 与圆
与圆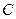 :
: 相交于
相交于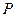 、
、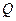 两点,点
两点,点 满足
满足 .
.
(Ⅰ)当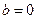 时,求实数
时,求实数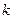 的值;
的值;
(Ⅱ)当 时,求实数
时,求实数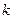 的取值范围;
的取值范围;
(Ⅲ)设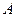 、
、 是圆
是圆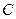 :
: 上两点,且满足
上两点,且满足 ,试问:是否存在一个定圆
,试问:是否存在一个定圆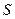 ,使直线
,使直线 恒与圆
恒与圆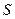 相切.
相切.
((本小题满分13分)
已知三个正数 满足
满足 .
.
(Ⅰ)若 是从
是从 中任取的三个数,求
中任取的三个数,求 能构成三角形三边长的概率;
能构成三角形三边长的概率;
(Ⅱ)若 是从区间
是从区间 内任取的三个数,求
内任取的三个数,求 能构成三角形三边长的概率.
能构成三角形三边长的概率.
((本小题满分12分 )
)
(Ⅰ)用分期付款方式购买家用电器一件,价格为 元,购买当天先付
元,购买当天先付
 元,以后每月这一天都交付
元,以后每月这一天都交付 元,并加付欠款利息,月利率为
元,并加付欠款利息,月利率为 .若交付
.若交付 元后的第一个月开始算分期付款的第一个月,全部欠款付清后,请问买这件家电实际付款多少元?
元后的第一个月开始算分期付款的第一个月,全部欠款付清后,请问买这件家电实际付款多少元?
(Ⅱ)用分期付款方式购买家用电器一件,价格为 元,购买当天先付
元,购买当天先付 元,以后每月这一天还款一次,每次还款数额相同,
元,以后每月这一天还款一次,每次还款数额相同,
 个月还清,月利率为
个月还清,月利率为 ,按复利计息.若交付
,按复利计息.若交付 元后的第一个月开始算分期付款的第一个月,全部欠款付清后,请问买这件家电实际付款多少元?每月还款多少元?(最后结果保留4个有
元后的第一个月开始算分期付款的第一个月,全部欠款付清后,请问买这件家电实际付款多少元?每月还款多少元?(最后结果保留4个有 效数字)
效数字)
参考数据: ,
, ,
, .
.
((本小题满分12分)
如图所示,正方形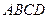 和矩形
和矩形 所在的平面相互垂直,已知
所在的平面相互垂直,已知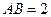 ,
, .
.
(Ⅰ)求证: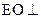 平面
平面 ;
;
(Ⅱ)求二面角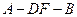 的大小.
的大小.