(本小题满分12分)设圆 过点P(0,2), 且在
过点P(0,2), 且在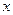 轴上截得的弦RG的长为4.
轴上截得的弦RG的长为4.
(Ⅰ)求圆心 的轨迹E的方程;
的轨迹E的方程;
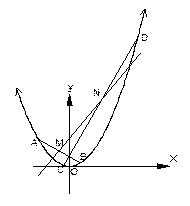
(Ⅱ)过点 (0,1),作轨迹
(0,1),作轨迹 的两条互相垂直的弦
的两条互相垂直的弦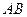 ,
,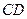 ,设
,设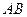 、
、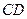 的中点分别为
的中点分别为 ,
,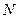 ,试判断直线
,试判断直线 是否过定点?并说明理由.
是否过定点?并说明理由.
已知数列 的前
的前 项和为
项和为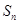 ,且满足
,且满足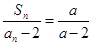 (
(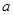 是常数且
是常数且 ,
,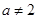 ),
),  .
.
(1)求数列 的通项公式;
的通项公式;
(2)若数列 为等比数列,求
为等比数列,求 的通项公式;
的通项公式;
(3)在(2)的条件下,记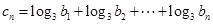
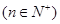 ,是否存在正整数
,是否存在正整数 ,使
,使 都成立?若存在,求出
都成立?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知函数 .
.
(1)求函数 的单调区间;
的单调区间;
(2)设函数 .若至少存在一个
.若至少存在一个 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
在等差数列 中,
中, ,其前
,其前 项和为
项和为 ,等比数列
,等比数列 的各项均为正数,
的各项均为正数, ,公比为
,公比为 ,且
,且 ,
, .
.
(1)求 与
与 ;
;
(2)设数列 满足
满足 ,求
,求 的前
的前 项和
项和 .
.
已知函数 .
.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)设 三内角
三内角 所对边分别为
所对边分别为 且
且 ,求
,求 在
在 上的值域.
上的值域.
现有4人去旅游,旅游地点有A,B两个地方可以选择.但4人都不知道去哪里玩,于是决定通过掷一枚质地均匀的骰子决定自己去哪里玩,掷出能被3整除的数时去A地,掷出其他的则去B地;
(1)求这4个人中恰好有1个人去B地的概率;
(2)求这4个人中去A地的人数大于去B地的人数的概率;
(3)用X,Y分别表示这4个人中去A,B两地的人数,记 .求随机变量
.求随机变量 的分布列与数学期望
的分布列与数学期望 .
.