(本小题满分13分)
某商场准备在国庆节期间举行促销活动,根据市场调查,该商场决定从2种服装商品,2种家电商品,3种日用商品中,选出3种商品进行促销活动.
(1)试求选出的3种商品中至少有一种是日用商品的概率;
(2)商场对选出的某商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高150元,同时,若顾客购买该商品,则允许有3次抽奖的机会,若中奖,则每次中奖都获得数额为 的奖金.假设顾客每次抽奖时获奖与否的概率都是
的奖金.假设顾客每次抽奖时获奖与否的概率都是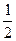 ,请问:商场应将每次中奖奖金数额
,请问:商场应将每次中奖奖金数额 最高定为多少元,才能使促销方案对商场有利?
最高定为多少元,才能使促销方案对商场有利?
如图,已知椭圆C的中心在原点O,焦点在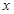 轴上,长轴长是短轴
轴上,长轴长是短轴
长的2倍,且经过点M . 平行于OM的直线
. 平行于OM的直线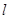 在
在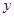 轴上的截距为
轴上的截距为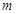
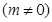 并交椭
并交椭
圆C于A、B两个不同点.
(1)求椭圆C的标准方程;
(2)求m的取值范围;
(3)求证:直线MA、MB与x轴始终围成一个等腰三角形. 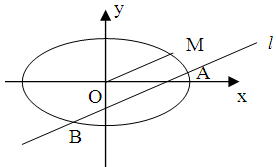
设定点M ,动点N在圆
,动点N在圆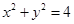 上运动,线段MN的
上运动,线段MN的
中点为点P.
(1)求MN的中点P的轨迹方程;
(2)直线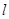 与点P的轨迹相切,且
与点P的轨迹相切,且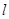 在
在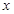 轴.
轴.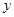 轴上的截距相等,求直线
轴上的截距相等,求直线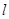 的方程.
的方程.
某工厂计划生产A.B两种涂料,生产A种涂料1t需要甲种原料
1t.乙种原料2t,可获利润3千元;生产B种涂料1t需要甲种原料2t,乙种原料1t,
可获利润2千元,又知该工厂甲种原料的用量不超过400t,乙种原料的用量不超过500t,
问如何安排生产才能获得最大利润?(注:t表示重量单位“吨”)
如果方程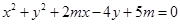 表示一个圆,
表示一个圆,
(1)求 的取值范围;
的取值范围;
(2)当m=0时的圆与直线 相交,求直线
相交,求直线 的倾斜角的取值范围.
的倾斜角的取值范围.
设集合A=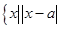 <
< ,集合B=
,集合B=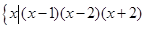 >
>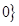 ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围.