(本小题满分13分)如图,由不大于n(n∈ )的正有理数排成的数表,质点按
)的正有理数排成的数表,质点按
 ……顺序跳动,
……顺序跳动,
所经过的有理数依次排列构成数列 。
。
(Ⅰ)质点从 出发,通过抛掷骰子来决定质点的跳动步数,骰子的点数为奇数时,质点往前跳一步(从
出发,通过抛掷骰子来决定质点的跳动步数,骰子的点数为奇数时,质点往前跳一步(从 到达
到达 );骰子的点数为偶数时,质点往前跳二步(从
);骰子的点数为偶数时,质点往前跳二步(从 到达
到达 ).
).
①抛掷骰子二次,质点到达的有理数记为ξ,求Eξ;②求质点恰好到达 的概率。
的概率。
(Ⅱ)试给出 的值(不必写出求解过程)。
的值(不必写出求解过程)。
(本小题满分12分)
在△ABC中,角A、B、C的对边分别为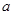 、
、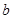 、
、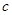 ,且满足
,且满足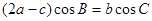 .
.
(1)求角B的大小;
|
(2)设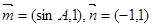 ,求
,求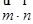 的最小值.
的最小值.
(本小题满分14分)
已知圆方程: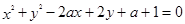 ,求圆心到直线
,求圆心到直线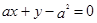 的距离的取值范围.
的距离的取值范围.
(本小题满分12分)
已知圆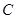 的方程为:
的方程为: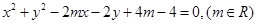 .
.
(1)试求 的值,使圆
的值,使圆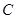 的面积最小;
的面积最小;
(2)求与满足(1)中条件的圆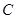 相切,且过点
相切,且过点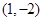 的直线方程.
的直线方程.
(本小题满分12分)
已知圆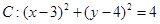 和直线
和直线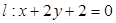 ,直线
,直线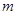 ,
,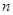 都经过圆C外定点A(1,0).
都经过圆C外定点A(1,0).
(Ⅰ)若直线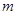 与圆C相切,求直线
与圆C相切,求直线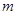 的方程;
的方程;
(Ⅱ)若直线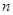 与圆C相交于P,Q两点,与
与圆C相交于P,Q两点,与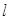 交于N点,且线段PQ的中点为M,
交于N点,且线段PQ的中点为M,
求证: 为定值.
为定值.
(本题满分12分)
已知直线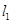 :
: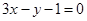 ,
,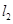 :
: ,求:
,求:
(1)直线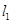 与
与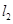 的交点
的交点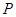 的坐标;(2)过点
的坐标;(2)过点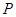 且与
且与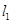 垂直的直线方程.
垂直的直线方程.