(请考生在以下三个小题中任选一题做答,如果多做,则按所做的第一题评阅记分)
(1)(选修4—4坐标系与参数方程)
已知曲线C的极坐标方程是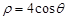 .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线 的参数方程是
的参数方程是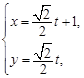 ,则直线
,则直线 与曲线C相交所成弦的弦长为 .
与曲线C相交所成弦的弦长为 .
(2)(选修4—5 不等式选讲)已知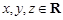 ,且
,且 ,则
,则 的最小值为 .
的最小值为 .
(3)(选修4—1 几何证明选讲)如图,若 ,
,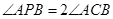 ,
, 与
与 交于点D,且
交于点D,且 ,
,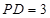 ,则
,则 .
.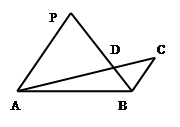
在数列 中,若
中,若 ,则称
,则称 为“等方差数列”,下列是对“等方差数列”的判断;
为“等方差数列”,下列是对“等方差数列”的判断;
①若 是等方差数列,则
是等方差数列,则 是等差数列;
是等差数列;
② 是等方差数列;
是等方差数列;
③若 是等方差数列,则
是等方差数列,则 也是等方差数列;
也是等方差数列;
④若 既是等方差数列,又是等差数列,则该数列为常数列。
既是等方差数列,又是等差数列,则该数列为常数列。
其中正确命题序号为。(将所有正确的命题序号填在横线上)
某校从参加高三年级期末考试的学生中抽出
60名学生,并统计了他们的历史成绩(成绩
均为整数且满分为100分),把其中不低于
50分的成绩分成五段 后,画出部分
后,画出部分
频率分布直方图(如图),那么历史成绩在 的学生人数为。
的学生人数为。
等差数列 中,
中, ,此数列的通项公式为,设
,此数列的通项公式为,设 是数列
是数列 的前
的前 项和,则
项和,则 等于。
等于。
函数 的最小正周期是,最大值是。
的最小正周期是,最大值是。
若 满足约束条件
满足约束条件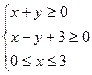 ,则
,则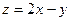 的最大值为。
的最大值为。