21.(本小题满分12分)
已知函数f(x)= 在x=1处取得极值(a>0)
在x=1处取得极值(a>0)
(I)求a、b所满足的条件;
(II)讨论函数f(x)的单调性.
已知函数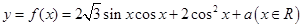 ,其中
,其中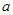 为常数.
为常数.
(1)求函数 的周期;
的周期;
(2)如果 的最小值为
的最小值为 ,求
,求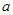 的值,并求此时
的值,并求此时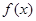 的最大值及图像的对称轴方程.
的最大值及图像的对称轴方程.
已知圆锥母线长为6,底面圆半径长为4,点 是母线
是母线 的中点,
的中点,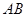 是底面圆的直径,半径
是底面圆的直径,半径 与母线
与母线 所成的角的大小等于
所成的角的大小等于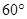 .
.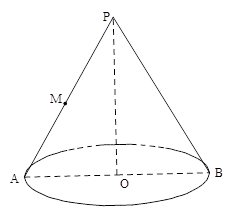
(1)求圆锥的侧面积和体积.
(2)求异面直线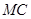 与
与 所成的角;
所成的角;
如图,直线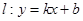 与抛物线
与抛物线 (常数
(常数 )相交于不同的两点
)相交于不同的两点 、
、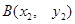 ,且
,且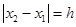 (
(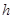 为定值),线段
为定值),线段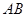 的中点为
的中点为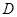 ,与直线
,与直线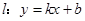 平行的切线的切点为
平行的切线的切点为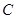 (不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
(不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
(1)用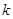 、
、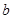 表示出
表示出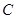 点、
点、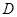 点的坐标,并证明
点的坐标,并证明 垂直于
垂直于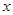 轴;
轴;
(2)求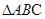 的面积,证明
的面积,证明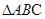 的面积与
的面积与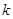 、
、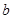 无关,只与
无关,只与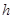 有关;
有关;
(3)小张所在的兴趣小组完成上面两个小题后,小张连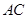 、
、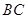 ,再作与
,再作与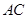 、
、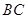 平行的切线,切点分别为
平行的切线,切点分别为 、
、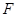 ,小张马上写出了
,小张马上写出了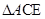 、
、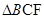 的面积,由此小张求出了直线
的面积,由此小张求出了直线 与抛物线围成的面积,你认为小张能做到吗?请你说出理由.
与抛物线围成的面积,你认为小张能做到吗?请你说出理由.
函数 的定义域为
的定义域为 ,若存在常数
,若存在常数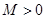 ,使得
,使得 对一切实数
对一切实数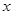 均成立,则称
均成立,则称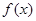 为“圆锥托底型”函数.
为“圆锥托底型”函数.
(1)判断函数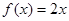 ,
,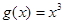 是否为“圆锥托底型”函数?并说明理由.
是否为“圆锥托底型”函数?并说明理由.
(2)若 是“圆锥托底型” 函数,求出
是“圆锥托底型” 函数,求出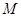 的最大值.
的最大值.
(3)问实数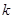 、
、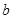 满足什么条件,
满足什么条件,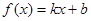 是“圆锥托底型” 函数.
是“圆锥托底型” 函数.
某市2013年发放汽车牌照12万张,其中燃油型汽车牌照10万张,电动型汽车2万张.为了节能减排和控制总量,从2013年开始,每年电动型汽车牌照按50%增长,而燃油型汽车牌照每一年比上一年减少 万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变.
万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变.
(1)记2013年为第一年,每年发放的燃油型汽车牌照数构成数列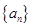 ,每年发放的电动型汽车牌照数为构成数列
,每年发放的电动型汽车牌照数为构成数列 ,完成下列表格,并写出这两个数列的通项公式;
,完成下列表格,并写出这两个数列的通项公式;
(2)从2013年算起,累计各年发放的牌照数,哪一年开始超过200万张?
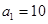 |
 |
 |
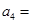 |
|
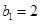 |
 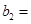 3 3 |
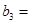 |
 |