(本题满分12分)

阅读以上流程图,若记y=f(x)
(1)写出y=f(x)的解析式,并求函数的值域,
(2)若x0满足f(x0)<0 且f(f(x0))=1,求x0.
已知等差数列 前三项的和为
前三项的和为 ,前三项的积为
,前三项的积为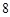 .
.
(1)求等差数列 的通项公式;
的通项公式;
(2)若 ,
,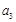 ,
,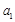 成等比数列,求数列
成等比数列,求数列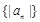 的前
的前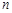 项和.
项和.
设函数 =
= -sin(2x-
-sin(2x-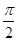 ).
).
(1)求函数 的最大值和最小值;
的最大值和最小值;
(2) 的内角
的内角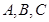 的对边分别为
的对边分别为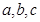 ,
,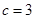 ,f(
,f( )=
)=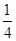 ,若
,若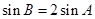 ,求
,求 的面积.
的面积.
已知顶点在原点,焦点在 轴上的抛物线被直线
轴上的抛物线被直线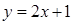 截得的弦长为
截得的弦长为 ,求抛物线的方程.
,求抛物线的方程.
已知偶函数 满足:当
满足:当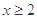 时,
时, ,当
,当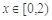 时,
时, .
.
(1)求当 时,
时, 的表达式;
的表达式;
(2)试讨论:当实数 满足什么条件时,函数
满足什么条件时,函数 有4个零点,且这4个零点从小到大依次构成等差数列.
有4个零点,且这4个零点从小到大依次构成等差数列.
已知函数 ,点
,点 为一定点,直线
为一定点,直线 分别与函数
分别与函数 的图象和
的图象和 轴交于点
轴交于点 ,
, ,记
,记 的面积为
的面积为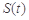 .
.
(1)当 时,求函数
时,求函数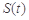 的单调区间;
的单调区间;
(2)当 时, 若
时, 若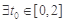 ,使得
,使得 , 求实数
, 求实数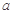 的取值范围.
的取值范围.