已知偶函数 满足:当
满足:当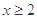 时,
时, ,当
,当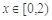 时,
时, .
.
(1)求当 时,
时, 的表达式;
的表达式;
(2)试讨论:当实数 满足什么条件时,函数
满足什么条件时,函数 有4个零点,且这4个零点从小到大依次构成等差数列.
有4个零点,且这4个零点从小到大依次构成等差数列.
已知函数
,其中
是自然对数的底数.
(1)证明:
是
上的偶函数;
(2)若关于
的不等式
在
上恒成立,求实数
的取值范围;
(3)已知正数
满足:存在
,使得
成立,试比较
与
的大小,并证明你的结论.
如图:为保护河上古桥
,规划建一座新桥
,同时设立一个圆形保护区,规划要求,新桥
与河岸
垂直;保护区的边界为圆心
在线段
上并与
相切的圆,且古桥两端
和
到该圆上任一点的距离均不少于
,经测量,点
位于点
正北方向
处,点
位于点
正东方向
处,(
为河岸),
.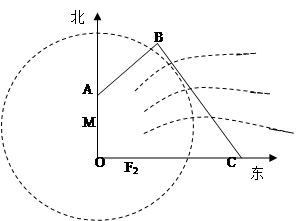
(1)求新桥
的长;
(2)当
多长时,圆形保护区的面积最大?
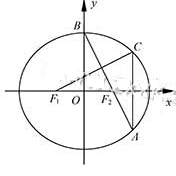
如图在平面直角坐标系
中,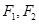 分别是椭圆
的左右焦点,顶点
的坐标是
,连接
并延长交椭圆于点
,过点
作
轴的垂线交椭圆于另一点
,连接
.
分别是椭圆
的左右焦点,顶点
的坐标是
,连接
并延长交椭圆于点
,过点
作
轴的垂线交椭圆于另一点
,连接
.
(1)若点
的坐标为
,且
,求椭圆的方程;
(2)若
,求椭圆离心率
的值.
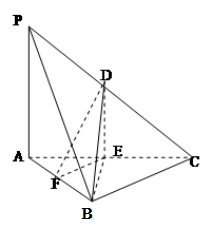
如图在三棱锥
中,
分别为棱
的中点,已知
.
求证:
(1)直线
平面
;
(2)平面
平面
.
已知
.
(1)求
的值;
(2)求