如图:为保护河上古桥,规划建一座新桥,同时设立一个圆形保护区,规划要求,新桥与河岸垂直;保护区的边界为圆心在线段上并与相切的圆,且古桥两端和到该圆上任一点的距离均不少于,经测量,点位于点正北方向处,点位于点正东方向处,(为河岸),.
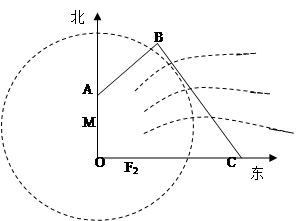
(1)求新桥的长;
(2)当多长时,圆形保护区的面积最大?
在直角坐标系xOy中,直线l的参数方程为 (t为参数).在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数).在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为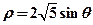
(1)求圆C的直角坐标方程;
(2)设圆C与直线l交于点A,B.若点P的坐标为(3, 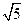 ),求|PA|+|PB|的值.
),求|PA|+|PB|的值.
给定两个命题, :对任意实数
:对任意实数 都有
都有 恒成立;
恒成立; :关于
:关于 的方程
的方程 有实数根;如果
有实数根;如果 与
与 中有且仅有一个为真命题,求实数
中有且仅有一个为真命题,求实数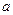 的取值范围.
的取值范围.
解关于x的不等式: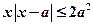

已知椭圆C: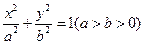 的长轴长为
的长轴长为 ,离心率
,离心率 .
.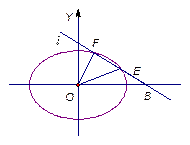
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若过点B(2,0)的直线 (斜率不等于零)与椭圆C交于不同的两点E,F(E在B,F之间),且
(斜率不等于零)与椭圆C交于不同的两点E,F(E在B,F之间),且 OBE与
OBE与 OBF的面积之比为
OBF的面积之比为 , 求直线
, 求直线 的方程.
的方程.
已知函数 ,其中
,其中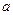 为大于零的常数.
为大于零的常数.
(Ⅰ)若曲线 在点(1,
在点(1, )处的切线与直线
)处的切线与直线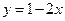 平行,求
平行,求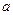 的值;
的值;
(Ⅱ)求函数 在区间[1,2]上的最小值.
在区间[1,2]上的最小值.