如图,DC⊥平面ABC,EB//DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE、AB的中点。
(I)证明:PQ//平面ACD;
(II)求异面直线AE与BC所成角的余弦值;
(III)求平面ACD与平面ABE所成锐二面角的大小。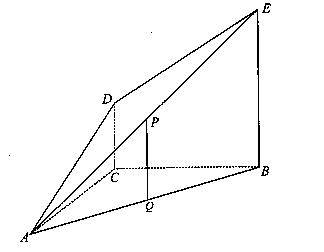
如图,在正方体 中,
中, 分别是
分别是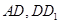 中点.
中点.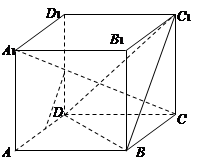
求证:(1)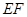 ∥平面
∥平面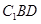 ;
;
(2)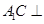 平面
平面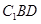 .
.
【原创】(本小题满分14分)设 是单位圆上三点,
是单位圆上三点, 为锐角.
为锐角.
(1)若 求
求
(2)若 求三角形
求三角形 面积的最大值.
面积的最大值.
设集合 ,
,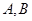 是
是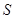 的两个非空子集,且满足集合
的两个非空子集,且满足集合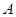 中的最大数小于集合
中的最大数小于集合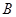 中的最小数,记满足条件的集合对
中的最小数,记满足条件的集合对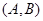 的个数为
的个数为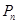 .
.
(1)求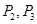 的值;
的值;
(2)求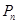 的表达式.
的表达式.
(本小题满分10分)某校开设8门校本课程,其中4门课程为人文科学,4门为自然科学,学校要求学生在高中三年内从中选修3门课程,假设学生选修每门课程的机会均等.
(1)求某同学至少选修1门自然科学课程的概率;
(2)已知某同学所选修的3门课程中有1门人文科学,2门自然科学,若该同学通过人文科学课程的概率都是 ,自然科学课程的概率都是
,自然科学课程的概率都是 ,且各门课程通过与否相互独立.用
,且各门课程通过与否相互独立.用 表示该同学所选的3门课程通过的门数,求随机变量
表示该同学所选的3门课程通过的门数,求随机变量 的概率分布列和数学期望。
的概率分布列和数学期望。
选修4—5:不等式选讲
已知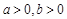 ,证明:
,证明: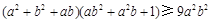 .
.