已知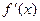 是
是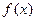 的导函数,
的导函数,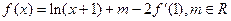 ,且函数
,且函数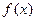 的图象过点(0,-2)。
的图象过点(0,-2)。
(1)求函数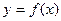 的表达式;
的表达式;
(2)设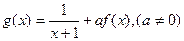 ,若
,若 在定义域内恒成立,求实数
在定义域内恒成立,求实数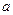 的取值范围。
的取值范围。
(本小题满分14分)
在 中,角
中,角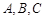 所对的边分别为
所对的边分别为 ,且
,且 成等差数列.
成等差数列.
(Ⅰ)求角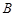 的大小
的大小
(Ⅱ)若 ,求
,求 边上中线长的最小值
边上中线长的最小值
(满分12分)) 设椭圆E:  (a,b>0)过
(a,b>0)过 (2,
(2, ) ,
) , (
( ,1)两点,O为坐标原点.
,1)两点,O为坐标原点.
(Ⅰ)求椭圆E的方程
(Ⅱ)是否存在圆心在原点的圆,使得该圆的任 意一条切线与椭圆E恒有两个交点A,B,
意一条切线与椭圆E恒有两个交点A,B,
且 ?若存在,写
?若存在,写 出该圆的方程,并求|AB |的取值范围,若不存在说明理由
出该圆的方程,并求|AB |的取值范围,若不存在说明理由
(满分12分)设等比数列 的各项均为正值,首项
的各项均为正值,首项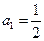 ,前n项和为
,前n项和为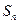 ,且
,且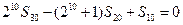
(Ⅰ)求 的通项;
的通项;
(Ⅱ)求 的前n项和
的前n项和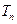 .
.
(满分12分)某家公司每 月生产两种布料A和B,所有原料是三种不同颜色的羊毛,下表给出了生产每匹每种布料所需的羊毛量,以及可供使用的每种颜色的羊毛的
月生产两种布料A和B,所有原料是三种不同颜色的羊毛,下表给出了生产每匹每种布料所需的羊毛量,以及可供使用的每种颜色的羊毛的 总量。
总量。
| 羊毛颜色 |
每 匹需要 / kg 匹需要 / kg |
供应量/ kg |
|
| 布料A |
布料B |
||
| 红 |
4 |
4 |
1400 |
| 绿 |
6 |
3 |
1800 |
| 黄 |
2 |
6 |
1800 |
已知生产每匹布料A、B的利润分别为120元、80元。那么如何安排生产才能够产生最大的利润?最 大的利润是多少?
大的利润是多少?
(满分12分)设锐角△ABC的内角A、B、C所对的边分别是a、b、c,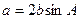 ,
,
(Ⅰ)求B的大小;
(Ⅱ)求cosA+sinC的取值范围。