(本小题满分14分)
如图,在直四棱柱 中,
中, ,
,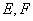 分别是
分别是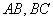 的中点.
的中点.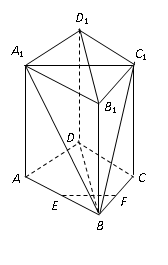
(Ⅰ)求证: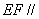 平面
平面 ;
;
(Ⅱ)求证:平面 平面
平面 .
.
已知集合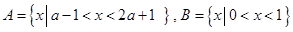 .
.
(Ⅰ)若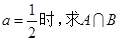 ;
;
(Ⅱ)若 ,求实数
,求实数 .
.
如图①正方形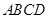 沿着对角线
沿着对角线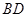 对折,并使平面
对折,并使平面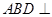 平面
平面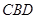 ,从而构成如图②三棱锥
,从而构成如图②三棱锥 ,点
,点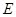 、
、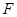 分别是线段
分别是线段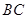 、
、 的中点.请在图②的三棱锥中解答如下问题:
的中点.请在图②的三棱锥中解答如下问题:
(1)求二面角 的正切值;
的正切值;
(2)求异面直线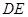 与
与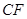 所成角的余弦值.
所成角的余弦值.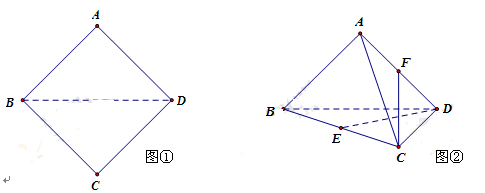
已知数列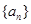 是各项均为正数的等差数列,其中
是各项均为正数的等差数列,其中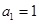 ,且
,且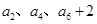 成等比数列;数列
成等比数列;数列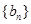 的前
的前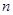 项和为
项和为 ,满足
,满足 .
.
(1)求数列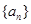 、
、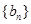 的通项公式;
的通项公式;
(2)如果 ,设数列
,设数列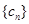 的前
的前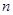 项和为
项和为 ,求证:
,求证: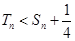 .
.
已知的顶点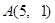 ,
,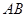 边上的中线
边上的中线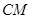 所在直线方程为
所在直线方程为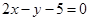 ,
,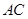 边上的高
边上的高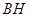 所在直线方程为
所在直线方程为 .
.
(1)求顶点 的坐标;
的坐标;
(2)求直线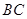 的一般方程.
的一般方程.
如图,三棱锥
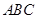 的三条侧棱两两垂直,即:
的三条侧棱两两垂直,即: 、
、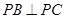 、
、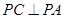 ,且
,且 平面
平面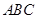 并交平面
并交平面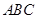 于点
于点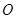 ,请问点
,请问点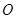 是
是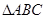 的什么心(内心、外心、垂心、重心、中心等)? 并证明你的结论.
的什么心(内心、外心、垂心、重心、中心等)? 并证明你的结论.