圆柱形容器，其底面直径为2m,深度为1 m,盛满液体后以0.01m3/s的速率放出，求液面高度的变化率.
已知函数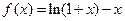
，求
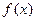的单调区间。
（本小题12分）
如图，在直三棱柱ABC—A1B1C1中，∠ACB=90°，AC=BC=CC1=2。
|
（1）证明：AB1⊥BC1；
（2）求点B到平面AB1C1的距离；（本小题12分）
已知椭圆的一个顶点为（－2，0)，焦点在x轴上，且离心率为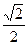
.
（1）求椭圆的标准方程.
（2）斜率为1的直线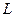
与椭圆交于A、B两点，O为原点，当△AOB的面积最大时，求直线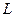的方程.
（本小题12分）
已知数列{an}中，a1 ="1" ，a2=3，且点（n，an）满足函数y =" kx" + b．
（1）求k ，b的值，并写出数列{an}的通项公式；
（2）记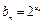
，求数列{bn}的前n和Sn ．
的铁皮截取一个以短轴
为底的等腰梯形
，问：怎样截才能使所得等腰梯形
