(本小题12分)
已知数列{an}中,a1 ="1" ,a2=3,且点(n,an)满足函数y =" kx" + b.
(1)求k ,b的值,并写出数列{an}的通项公式;
(2)记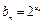 ,求数列{bn}的前n和Sn .
,求数列{bn}的前n和Sn .
已知函数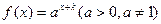 的图象过(-1,1)点,其反函数
的图象过(-1,1)点,其反函数 的图象过(8,2)点。
的图象过(8,2)点。
(1)求a,k的值;
(2)若将 的图象向在平移两个单位,再向上平移1个单位,就得到函数
的图象向在平移两个单位,再向上平移1个单位,就得到函数 的图象,写出
的图象,写出 的解析式;
的解析式;
(3)若函数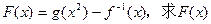 的最小值及取最小值时x的值。
的最小值及取最小值时x的值。
已知函数 的图象上以N(1,n)为切点的切线倾斜角为
的图象上以N(1,n)为切点的切线倾斜角为 .
.
(1)求m,n的值;
(2)是否存在最小的正整数k,使得不等式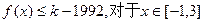 恒成立?若存在,求出最小的正整数k,否则请说明理由.
恒成立?若存在,求出最小的正整数k,否则请说明理由.
甲、乙两个粮库要向A、B两镇运送大米,已知甲库可调出100t大米,乙库可调出80t大米,A镇需70t大米,B镇需110t大米,两库到两镇的路程和运费如下表:
| 路程/km |
运费/(元·t-1·km-1) |
|||
| 甲库 |
乙库 |
甲库 |
乙库 |
|
| A镇 |
20 |
15 |
12 |
12 |
| B镇 |
25 |
20 |
10 |
8 |
(1)这两个粮库各运往A、B两镇多少t大米,才能使总运费最省?此时总运费是多少?
(2)最不合理的调运方案是什么?它使国家造成的损失是多少?
对于函数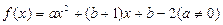 ,若存在实数
,若存在实数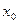 ,使
,使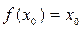 成立,则称
成立,则称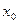 为
为 的不动点.
的不动点.
(1)当 时,求
时,求 的不动点;
的不动点;
(2)若对于任何实数 ,函数
,函数 恒有两相异的不动点,求实数
恒有两相异的不动点,求实数 的取值范围;
的取值范围;
(3)在(2)的条件下,若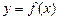 的图象上
的图象上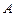 、
、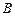 两点的横坐标是函数
两点的横坐标是函数 的不动点,且直线
的不动点,且直线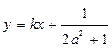 是线段
是线段 的垂直平分线,求实数
的垂直平分线,求实数 的最小值.
的最小值.
已知点M(-2,0),N(2,0),动点P满足条件 ,该动点的轨迹为F,
,该动点的轨迹为F,
(1)求F的方程。
(2)若A、B是F上的不同两点,O是坐标原点,求 的最小值。
的最小值。