(本小题14分)设函数

(1)若 时函数
时函数 有三个互不相同的零点,求
有三个互不相同的零点,求 的范围;
的范围;
(2)若函数 在
在 内没有极值点,求
内没有极值点,求 的范围;
的范围;
(3)若对任意的 ,不等式
,不等式 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
集合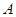 ={
={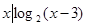
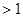 },
},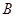 ={
={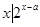
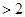 },
},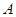
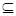
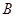 ,求实数
,求实数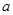 的取值范围
的取值范围
已知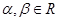 ,写出用
,写出用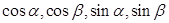 表示
表示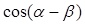 的关系等式,并证明这个关系等式.
的关系等式,并证明这个关系等式.
如图,在直三棱柱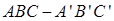 中,
中,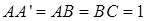 ,
,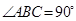 .棱
.棱 上有两个动点E,F,且EF =" a" (a为常数).
上有两个动点E,F,且EF =" a" (a为常数).
(Ⅰ)在平面ABC内确定一条直线,使该直线与直线CE垂直;
(Ⅱ)判断三棱锥B—CEF的体积是否为定值.若是定值,求出这个三棱锥的体积;若不是定值,说明理由.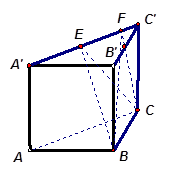
记等差数列{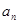 }的前n项和为
}的前n项和为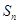 ,已知
,已知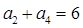 ,
,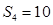 .
.
(Ⅰ)求数列{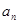 }的通项公式;
}的通项公式;
(Ⅱ)令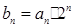
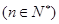 ,求数列{
,求数列{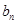 }的前项和
}的前项和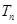 .
.
一种放射性元素,最初的质量为500g,按每年10﹪衰减.
(Ⅰ)求t年后,这种放射性元素质量ω的表达式;
(Ⅱ)由求出的函数表达式,求这种放射性元素的半衰期(剩留量为原来的一半所需要的时间).(精确到0.1;参考数据: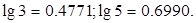 )
)