足够长的光滑平行金属导轨
和
水平放置，在其左端固定一个倾角为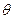
的光滑金属导轨，导轨相距均为
,在水平导轨和倾斜导轨上，各有一根与导轨垂直的金属杆，两金属杆与水平导轨、倾斜导轨形成—闭合回路。两金属杆质量均为
、电阻均为
,其余电阻不计，杆
被销钉固定在倾斜导轨某处。整个装置处于匀强磁场中，磁感应强度为
，方向竖直向上。当用水平向右、大小
的恒力拉杆
，使其达到最大速度时，立即撤去销钉，发现杆恰好能在原处仍然保持静止。（重力加速度为
）
（1）求杆运动中的最大速度
。
（2）求倾斜导轨的倾角。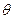
（3）若杆加速过程中发生的位移为
，则杆加速过程中，求杆上产生的热量
。
如图所示，一条小河两岸的高度差
，一辆摩托车（可看作质点）以
的水平速度向河对岸飞出，恰好越过小河．不计空气阻力，取当地的重力加速度
．试求：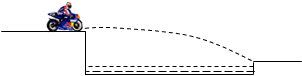
（1）摩托车在空中的飞行时间；
（2）小河的宽度．
（1）开普勒行星运动第三定律指出：行星绕太阳运动的椭圆轨道的半长轴 的三次方与它的公转周期T的二次方成正比，即 ， 是一个对所有行星都相同的常量。将行星绕太阳的运动按圆周运动处理，请你推导出太阳系中该常量 的表达式。已知引力常量为 ，太阳的质量为 。
（2）开普勒定律不仅适用于太阳系，它对一切具有中心天体的引力系统（如地月系统）都成立。经测定月地距离为
，月球绕地球运动的周期为
，试计算地球的质量
。（
，结果保留一位有效数字）
如图所示，甲为某一波在t＝1.0 s时的图象，乙为参与该波动的P质点的振动图象．
(1)试确定波的传播方向；
(2)求该波的波速v；
(3)在甲图中画出3.5 s时的波形图；
(4)求再经过3.5 s时P质点的路程s和位移．
一列简谐横波在t1=0时刻的波形图如图7-13所示，已知该波沿x轴正方向传播，在t2=0.7s末时，质点P刚好出现第二次波峰，试求：
（1）波速υ.
（2）x坐标为6m的Q点第一次出现波谷的时刻t3=?
如图所示，A、B两物体的质量都为m，拉A物体的细线与水平方向的夹角为30°时处于静止状态，不考虑摩擦力，设弹簧的劲度系数为k。若将悬线突然剪断，A在水平面上做周期为T的简谐运动，当B落地时，A恰好将弹簧压缩到最短，求：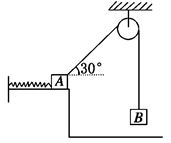
(1)A振动时的振幅；
(2)B落地时的速度．