（本小题满分12分）
上海世博会于2010年5月1日正式开幕，按规定个人参观各场馆需预约，即进入园区后持门票当天预约，且一张门票每天最多预约六个场馆。考虑到实际情况（排队等待时间等），张华决定参观甲、乙、丙、丁四个场馆。假设甲、乙、丙、丁四个场馆预约成功的概率分别是
且它们相互独立互不影响。
（1）求张华能成功预约甲、乙、丙、丁中两个场馆的概率；
（2）用
表示能成功预约场馆的个数，求随机变量的分布列和数学期望。
已知函数
，其中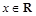
，
．
(Ⅰ)若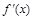
的最小值为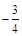
，试判断函数
的零点个数，并说明理由；
(Ⅱ)若函数的极小值大于零，求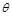
的取值范围．
设等差数列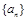
的前n项和为
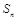，且
，
．
（Ⅰ）求数列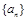的通项公式；
（Ⅱ）设数列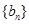
前n项和为
，且
，令
．求数列
的前n项和
.
在△ABC中，角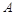
、
、
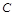的对边分别为
、
、
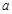，设S为△ABC的面积，满足
．
(Ⅰ)求角C的大小；
(Ⅱ)若
，且
，求的值．
在一次数学统考后，某班随机抽取10名同学的成绩进行样本分析，获得成绩数据的茎叶图如下．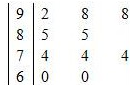
（Ⅰ）计算样本的平均成绩及方差；
（Ⅱ）现从80分以上的样本中随机抽出2名学生，求抽出的2名学生的成绩分别在
、
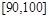上的概率．
已知函数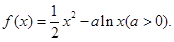
（Ⅰ）若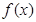
在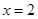
处的切线与直线
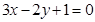平行，求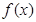的单调区间；
（Ⅱ）求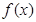在区间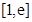
上的最小值.