已知随机变量
的分布列如下表，则随机变量的方差
的最大值为（ ）
 |
0 |
1 |
2 |
| P |
y |
0．4 |
x |
A．
B．0．6 C
．
D．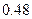
用数学归纳法证明：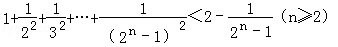
（n∈N*）时第一步需要证明（）
A． |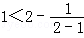
B． |
C． |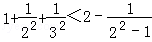
D． |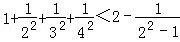
用数学归纳法证明不等式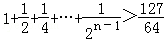
成立，起始值至少应取为（）
| A．7 | B．8 | C．9 | D．10 |
用数学归纳法证明“1+
+
+…+
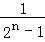＜n（n∈N*，n＞1）”时，由n=k（k＞1）不等式成立，推证n=k+1时，左边应增加的项数是（）
| A．2k﹣1 | B．2k﹣1 | C．2k | D．2k+1 |
用数学归纳法证明等式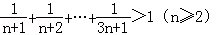
的过程中，由n=k递推到n=k+1时不等式左边（）
| A．增加了项 | B．增加了项  |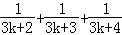
| C．增加了项 | D．以上均不对 |
一个关于自然数n的命题，如果验证当n=1时命题成立，并在假设当n=k（k≥1且k∈N*）时命题成立的基础上，证明了当n=k+2时命题成立，那么综合上述，对于（）
| A．一切正整数命题成立 | B．一切正奇数命题成立 |
| C．一切正偶数命题成立 | D．以上都不对 |