建造一个容积为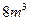 ,深为2m的长方体无盖水池,如果池底的造价为每平方米120元,池壁的造价为每平方米80元,求这个水池的最低造价
,深为2m的长方体无盖水池,如果池底的造价为每平方米120元,池壁的造价为每平方米80元,求这个水池的最低造价
在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=1.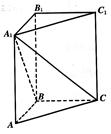
(1)求异面直线B1C1与AC所成角的大小;
(2)若该直三棱柱ABC-A1B1C1的体积为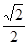 ,求点A到平面A1BC的距离.
,求点A到平面A1BC的距离.
已知函数
(1)求函数 的值域,并写出函数
的值域,并写出函数 的单调递增区间;
的单调递增区间;
(2)若 ,且
,且 ,计算
,计算 的值.
的值.
已知点 ,点
,点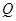 在曲线
在曲线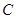 :
: 上.
上.
(1)若点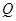 在第一象限内,且
在第一象限内,且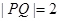 ,求点
,求点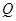 的坐标;
的坐标;
(2)求 的最小值.
的最小值.
定义在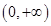 上的函数
上的函数 ,如果对任意
,如果对任意 ,恒有
,恒有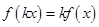 (
(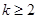 ,
, )成立,则称
)成立,则称 为
为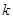 阶缩放函数.
阶缩放函数.
(1)已知函数 为二阶缩放函数,且当
为二阶缩放函数,且当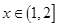 时,
时, ,求
,求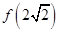 的值;
的值;
(2)已知函数 为二阶缩放函数,且当
为二阶缩放函数,且当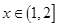 时,
时,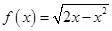 ,求证:函数
,求证:函数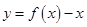 在
在 上无零点;
上无零点;
(3)已知函数 为
为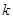 阶缩放函数,且当
阶缩放函数,且当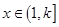 时,
时, 的取值范围是
的取值范围是 ,求
,求 在
在 (
(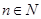 )上的取值范围.
)上的取值范围.
已知数列 中,
中, ,
, ,
, .
.
(1)证明:数列 是等比数列,并求数列
是等比数列,并求数列 的通项公式;
的通项公式;
(2)在数列 中,是否存在连续三项成等差数列?若存在,求出所有符合条件的项;若不存在,请说明理由;
中,是否存在连续三项成等差数列?若存在,求出所有符合条件的项;若不存在,请说明理由;
(3)若 且
且 ,
, ,求证:使得
,求证:使得 ,
, ,
, 成等差数列的点列
成等差数列的点列 在某一直线上.
在某一直线上.