(本题满分12分)在某次射击比赛中共有5名选手，出场时甲、乙、丙三人不能相邻。求（1）共有多少种不同的出场顺序？
（2）若甲、乙、丙三人每次射击命中目标的概率都为0.6,求三人各射击一次至少有一
人命中目标的概率。
（3）若甲、乙、丙三人每次射击命中目标的概率分别为0.7,0.6,0.5，求三人各射击一
次至少有两人命中目标的概率。
一束光线l自A（－3，3）发出，射到x轴上，被x轴反射到⊙C：x2＋y2－4x－4y＋7＝0上．（1）求反射线通过圆心C时，光线l的方程；（2）求在x轴上，反射点M的范围．
如图,四棱锥P—ABCD的底面ABCD为正方形，PD⊥底面ABCD，PD=AD.求证：（1）平面PAC⊥平面PBD；（2）求PC与平面PBD所成的角；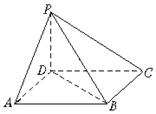
已知函数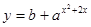
(
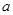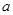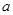、b是常数且>0，≠1)在区间[－
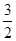，0]上有ymax=3，ymin=
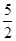，试求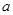和b的值.[
．求经过点A（-5，2）且在x轴上的截距等于在y轴上的截距的2倍的直线方程；
(本小题满分7分)选修4—5：不等式选讲
已知a2+b2+c2=1(a，b，c∈
)，求a+b+c的最大值．