(本小题满分13分)
设函数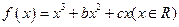 ,已知
,已知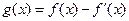 是奇函数.
是奇函数.
(Ⅰ)求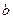 、
、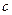 的值; (Ⅱ)求
的值; (Ⅱ)求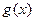 的单调区间与极值.
的单调区间与极值.
为了让学生更多的了解“数学史”知识,某中学高二年级举办了一次“追寻先哲的足迹,倾听数学的声音”的数学史知识竞赛活动,共有800名学生参加了这次竞赛,为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,统计结果见下表。请你根据频率分布表解答下列问题:
(1)填充频率分布表中的空格。
(2)为鼓励学生更多的学生了解“数学史”知识,成绩不低于85分的同学能获奖,请估计在参加的800名学生中大概有多少名学生获奖?
(3)在上述统计数据的分析中有一项计算见算法流程图,求输出的S的值. 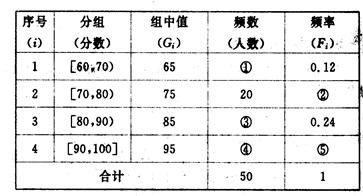

下表提供了某厂节能降耗技术发行后,生产甲产品过程中记录的产量 (吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
| x |
3 |
4 |
5 |
6 |
| y |
2.5 |
3 |
4 |
4.5 |
(1)求线性回归方程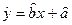 所表示的直线必经过的点;
所表示的直线必经过的点;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 ;
;
并预测生产1000吨甲产品的生产能耗多少吨标准煤?
(参考: )
)
(本小题满分14分)
已知数列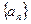 中,
中,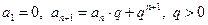 ,
,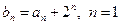 ,2,3,…
,2,3,…
(I)求证数列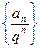 是等差数列;
是等差数列;
(II)试比较 的大小;
的大小;
(III)求正整数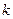 ,使得对于任意的正整数
,使得对于任意的正整数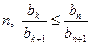 恒成立。
恒成立。
(本小题满分14分)
设函数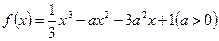 。
。
(I)求函数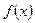 的单调区间、极大值和极小值。
的单调区间、极大值和极小值。
(II)若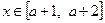 时,恒有
时,恒有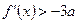 ,求实数
,求实数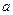 的取值范围。
的取值范围。
(本小题满分13分)
已知等差数列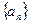 的前
的前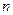 项和为
项和为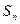 ,已知
,已知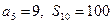 。
。
(I)求通项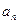 ;
;
(II)记数列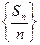 的前
的前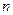 项和为
项和为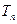 ,数列
,数列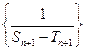 的前
的前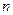 项和为
项和为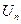 ,求证:
,求证: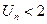 。
。