(本小题满分12分)
某单位组织职工参加了旨在调查职工健康状况的测试.该测试包括心理健康测试和身体健康两个项目,每个项目的测试结果为A、B、C、D、E五个等级.假设该单位50位职工全部参加了测试,测试结果如下:x表示心理健康测试结果,y表示身体健康测试结果.
 y y人数 x |
身体健康 |
|||||
| A |
B |
C |
D |
E |
||
| 心理健康 |
A |
1 |
3 |
1 |
0 |
1 |
| B |
1 |
0 |
7 |
5 |
1 |
|
| C |
2 |
1 |
0 |
9 |
3 |
|
 D D |
1 |
b |
6 |
0 |
a |
|
| E |
0 |
0 |
1 |
1 |
3 |
(I)求a+b的值;
(II)如果在该单位随 机找一位职工谈话,求找到的职工在这次测试中心理健康为D等且身体健康为C等的概率;
机找一位职工谈话,求找到的职工在这次测试中心理健康为D等且身体健康为C等的概率;
(III)若“职工的心理健康为D等”与“职工的身体健康为B等”是相互独立事件,求a、b的值.
已知直三棱柱 的三视图如图所示,
的三视图如图所示,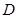 是
是 的中点.
的中点.
(Ⅰ)求证: ∥平面
∥平面 ;
;
(Ⅱ)求二面角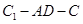 的余弦值;
的余弦值;
(Ⅲ)试问线段 上是否存在点
上是否存在点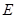 ,使
,使 与
与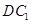 成
成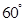 角?若存在,确定
角?若存在,确定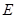 点位置,若不存在,说明理由.
点位置,若不存在,说明理由.
今年我国部分省市出现了人感染H7N9禽流感确诊病例,各地家禽市场受其影响生意冷清.A市虽未发现H7N9疑似病例,但经抽样有20%的市民表示还会购买本地家禽.现将频率视为概率,解决下列问题:
(Ⅰ)从该市市民中随机抽取3位,求至少有一位市民还会购买本地家禽的概率;
(Ⅱ)从该市市民中随机抽取 位,若连续抽取到两位愿意购买本地家禽的市民,或
位,若连续抽取到两位愿意购买本地家禽的市民,或
抽取的人数达到4位,则停止抽取,求 的分布列及数学期望.
的分布列及数学期望.
已知ΔABC中,满足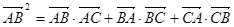 ,a,b,c分别是ΔABC的三边。
,a,b,c分别是ΔABC的三边。
(1)试判定ΔABC的形状,并求sinA+sinB的取值范围。
(2)若不等式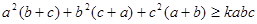 对任意的a,b,c都成立,求实数k的取值范围。
对任意的a,b,c都成立,求实数k的取值范围。
如图,圆 与离心率为
与离心率为 的椭圆
的椭圆 (
( )相切于点
)相切于点 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点 引两条互相垂直的两直线
引两条互相垂直的两直线 、
、 与两曲线分别交于点
与两曲线分别交于点 、
、 与点
与点 、
、 (均不重合).
(均不重合).
(ⅰ)若 为椭圆上任一点,记点
为椭圆上任一点,记点 到两直线的距离分别为
到两直线的距离分别为 、
、 ,求
,求 的最大值;
的最大值;
(ⅱ)若 ,求
,求 与
与 的方程.
的方程.
已知函数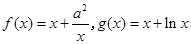 ,其中
,其中 .
.
(Ⅰ)若 是函数
是函数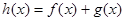 的极值点,求实数
的极值点,求实数 的值;
的值;
(Ⅱ)若对任意的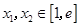 (
(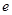 为自然对数的底数)都有
为自然对数的底数)都有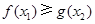 成立,求实数
成立,求实数 的取值范围.
的取值范围.