如图,在矩形 中,
中, ,
, ,
, 是
是 的中点,以
的中点,以 为折痕将
为折痕将 向上折起,使
向上折起,使 为
为 ,且平面
,且平面 平面
平面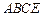
(Ⅰ)求证: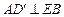 ;
;
(Ⅱ)求二面角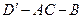 的大小;
的大小;
(Ⅲ)求点C到面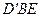 的距离.
的距离. 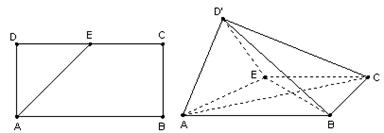
(本题满分12分)
阅读右图的流程图.
(1)写出函数y = f (x)的解析式;
(2)由(1)中的函数y = f (x)表示的曲线与直线y =1围成的三角
形的内切圆记为圆O,若向这个三角形内投掷一个点,求这
个点落入圆O内的概率.
(本小题满分12分)
一个口袋内装有大小相同的2个白球和3个黑球.
(1)从中一次摸出两个球,求两球都是黑球的概率;
(2)从中一次摸出两个球,求两球恰好颜色不同的概率.
(本小题满分10分)
已知集合A={x|a≤x≤a+2},B={x|x<-1或x>5}.
(1)若a=-2,求集合A∩B;
(2)若A∪B=B,求实数a的取值范围.
在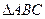 中,角
中,角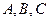 所对的边分别是
所对的边分别是 ,
,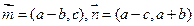 ,且
,且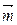 与
与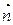 共线.
共线.
⑴求角 的大小;
的大小;
⑵设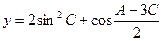 ,求
,求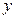 的最大值及此时
的最大值及此时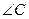 的大小.
的大小.
在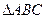 中,角
中,角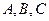 所对的边分别是
所对的边分别是 ,若
,若
⑴判断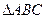 的形状;
的形状;
⑵若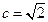 ,求
,求 的值.
的值.