(本小题满分10分)选修4-4:坐标系与参数方程
已知曲线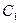 的极坐标方程为
的极坐标方程为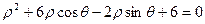 ,曲线
,曲线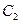 的参数方程为
的参数方程为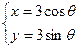 (
(
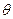 为参
为参 数).
数).
(Ⅰ) 将曲线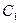 的极
的极 坐标方程化为直角坐标方程;
坐标方程化为直角坐标方程;
(Ⅱ) 曲 线
线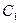 和曲线
和曲线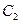 交于
交于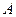 、
、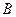 两点,求
两点,求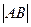 长.
长.
已知△ABC中, ,
, ,且
,且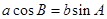 .
.
(1)求∠B的值;
(2)若点E,P分别在边AB,BC上,且AE=4,AP⊥CE,求AP的长;
已知等差数列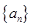 满足
满足 .
.
(1)求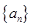 的通项公式;
的通项公式;
(2)求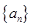 的前
的前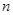 项和
项和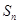 ;
;
(3)若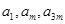 成等比数列,求
成等比数列,求 的值.
的值.
已知函数 .
.
(1)求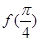 值;
值;
(2)求 的最小值正周期;
的最小值正周期;
(3)求 的单调递增区间.
的单调递增区间.
已知函数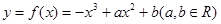
(1)若函数 的图象切x轴于点(2,0),求a、b的值;
的图象切x轴于点(2,0),求a、b的值;
(2)设函数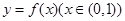 的图象上任意一点的切线斜率为k,试求
的图象上任意一点的切线斜率为k,试求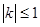 的充要条件;
的充要条件;
(3)若函数 的图象上任意不同的两点的连线的斜率小于l,求证
的图象上任意不同的两点的连线的斜率小于l,求证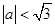 .
.
给定椭圆 .称圆心在原点O,半径为
.称圆心在原点O,半径为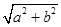 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为 ,其短轴上的一个端点到F的距离为
,其短轴上的一个端点到F的距离为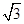 .
.
(1)求椭圆C的方程和其“准圆”方程;
(2)点P是椭圆C的“准圆”上的一个动点,过动点P作直线 ,使得
,使得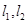 与椭圆C都只有一个交点,试判断
与椭圆C都只有一个交点,试判断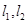 是否垂直?并说明理由.
是否垂直?并说明理由.