如下图所示，在等腰梯形
中，
为
边上一点，
且
将
沿
折起，使平面
⊥平面
．
(1)求证：
⊥平面；
(2)若
是侧棱中点，求截面
把几何体分成的两部分的体积之比。
（本小题
满分12分）
已知函数
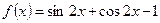
（1）求函数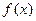
的单调增区间；
（2）求函数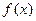的最大值及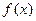取最大值时x的集合。
（本小题满分12分）
如图，某地一天中6时至14时的温度变化曲线近
似满足函数
（其中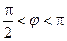 
），
（1）求这一天6时至14时的最大温差；
（2）求与图中曲线对应的函数解析式.
（本小题满分12
分）
已知非零向量
、
满足
，且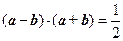
.
（1）求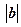
；
（2）当
时，求向量与的夹角
的值.
（本小题满分10分）
已知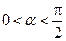
,
.
（1）求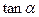
的值；
（2）求
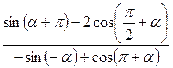的值.
（满分20分）本题有2小题，第1小题12分，第2小题8分．
已知数列{
}和{
}满足：对于任何
，有
，
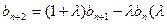为非零常数），且
．
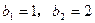（1）求数列{}和{}的通项公式；
（2）若
是
与
的等差中项，试求
的值，并研究：对任意的，是否一定能是数列{}中某两项（不同于）的等差中项，并证明你的结论．