(本题满分10分) 在等比数列 中,
中, (
( )
)
(Ⅰ)求数列 的通项公式
的通项公式 ;
;
(2)求数列 的前n项和
的前n项和 ;
;
(3)令 求数列
求数列 的前
的前 项和
项和 。
。
如图(1),在等腰直角三角形 中,
中,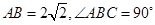 ,点
,点 分别为线段
分别为线段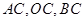 的中点,将
的中点,将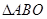 和
和 分别沿
分别沿 折起,使二面角
折起,使二面角 和二面角
和二面角 都成直二面角,如图(2)所示。
都成直二面角,如图(2)所示。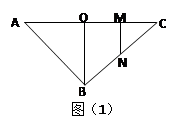

(1)求证: 面
面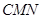 ;
;
(2)求平面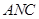 与平面
与平面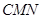 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;
(3)求点 到平面
到平面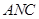 的距离。
的距离。
已知函数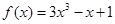 。
。
(1)求函数 的单调递减区间;
的单调递减区间;
(2)求切于点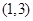 的切线方程;
的切线方程;
(3)求函数 在
在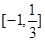 上的最大值与最小值。
上的最大值与最小值。
平面内动点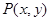 到定点
到定点 的距离比它到
的距离比它到 轴的距离大
轴的距离大 。
。
(1)求动点 的轨迹
的轨迹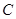 的方程;
的方程;
(2)过 的直线
的直线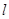 与
与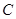 相交于
相交于 两点,若
两点,若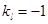 ,求弦
,求弦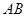 的长。
的长。
对于无穷数列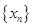 和函数
和函数 ,若
,若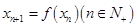 ,则称
,则称 是数列
是数列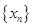 的母函数.
的母函数.
(Ⅰ)定义在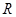 上的函数
上的函数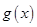 满足:对任意
满足:对任意 ,都有
,都有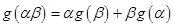 ,且
,且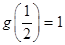 ;又数列
;又数列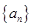 满足:
满足: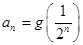 .
.
求证:(1)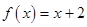 是数列
是数列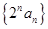 的母函数;
的母函数;
(2)求数列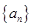 的前项
的前项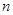 和
和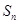 .
.
(Ⅱ)已知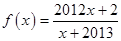 是数列
是数列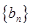 的母函数,且
的母函数,且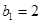 .若数列
.若数列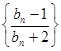 的前
的前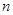 项和为
项和为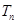 ,求证:
,求证: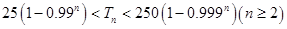 .
.
已知数列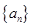 的前
的前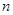 项和
项和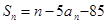 ,
,
(Ⅰ)求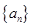 的通项公式;
的通项公式;
(Ⅱ) 令 ,求数列
,求数列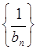 的前
的前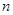 项和
项和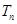 .
.