已知数列{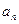 }中,
}中,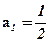 ,点
,点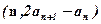 在直线y=x上,其中n=1,2,3….
在直线y=x上,其中n=1,2,3….
(Ⅰ)令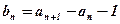 ,求证数列
,求证数列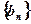 是等比数列;
是等比数列;
(Ⅱ)求数列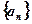 的通项;
的通项;
(Ⅲ)设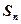 、
、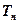 分别为数列
分别为数列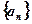 、
、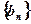 的前n项和,是否存在实数
的前n项和,是否存在实数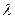 ,使得数列
,使得数列 为等差数列?若存在,试求出
为等差数列?若存在,试求出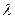 ,若不存在,则说明理由。
,若不存在,则说明理由。
(本小题满分12分)已知函数 -
-
(1)求 的最小正周期及其对称中心;
的最小正周期及其对称中心;
(2)如果三角形ABC的三边a、b、c满足b2=ac,且边b所对角为x,试求x的范围及此时函数 的值域.
的值域.
(本小题满分12分)如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
(1)若PA=PD,求证:平面PQB⊥平面PAD;
(2)若平面PAD⊥平面ABCD,且PA=PD=AD=2,点M在线段PC上,且PM=3MC,求三棱锥P﹣QBM的体积.
(本小题满分12分)
设数列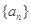 的前
的前 项和
项和 ,且
,且 成等差数列.
成等差数列.
(1)求数列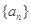 的通项公式;
的通项公式;
(2)记数列 的前n项和
的前n项和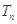 ,求得
,求得 成立的n的最小值.
成立的n的最小值.
(本小题满分10分)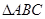 的内角A、B、C的对边分别为a、b、c,已知
的内角A、B、C的对边分别为a、b、c,已知 ,
, ,求B.
,求B.
(本小题满分10分)【选修4-5:不等式选讲】
设f(x)=|x+2|+|2x-1|-m.
(1)当m=5时.解不等式f(x)≥0;
(2)若f(x)≥ ,对任意
,对任意 恒成立,求m的取值范围.
恒成立,求m的取值范围.