某工厂师徒二人各加工相同型号的零件2个,是否加工出精品均互不影响.已知师父加工一个零件是精品的概率为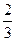 ,师徒二人各加工2个零件都是精品的概率为
,师徒二人各加工2个零件都是精品的概率为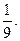 (I)求徒弟加工2个零件都是精品的概率;
(I)求徒弟加工2个零件都是精品的概率;
(II)求徒弟加工该零件的精品数多于师父的概率;
(III)设师徒二人加工出的4个零件中精品个数为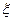 ,求
,求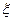 的分布列与均值E
的分布列与均值E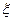
某商场从生产厂家以每件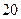 元购进一批商品,若该商品零售价为
元购进一批商品,若该商品零售价为 元,则销售量
元,则销售量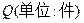 与零售价
与零售价 (单位:元)有如下关系:
(单位:元)有如下关系: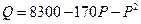 。问该商品零售价定为多少时,毛利润
。问该商品零售价定为多少时,毛利润 最大,并求最大利润(毛利润
最大,并求最大利润(毛利润 销售收入
销售收入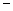 进货支出)
进货支出)
用总长为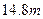 的钢条制作一个长方体容器的框架,如果所制作的容器的底面的一边比另一边长
的钢条制作一个长方体容器的框架,如果所制作的容器的底面的一边比另一边长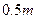 ,那么高为多少时容器的容积最大?并求出它的最大体积。
,那么高为多少时容器的容积最大?并求出它的最大体积。
已知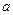 为实数,
为实数, 。(1)求导数
。(1)求导数 ;(2)若
;(2)若 ,求
,求 在
在 上的最大值和最小值;(3)若
上的最大值和最小值;(3)若 在
在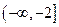 和
和 上都是递增函数,求
上都是递增函数,求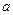 的取值范围。
的取值范围。
一火车锅炉每小时消耗的费用与火车行驶的速度的立方成正比,已知当速度为每小时 时,每小时消耗的煤价值
时,每小时消耗的煤价值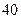 元,至于其他费用每小时要
元,至于其他费用每小时要 元,问火车行驶的速度为多少时,才能使火车从甲城开往乙城的总费用最省?
元,问火车行驶的速度为多少时,才能使火车从甲城开往乙城的总费用最省?
做一个容积为 的有盖方底的水箱,它的底边长为多少时,用料最省?
的有盖方底的水箱,它的底边长为多少时,用料最省?