(本小题满分12分) 甲、乙、丙三人按下面的规则进行乒乓球比赛: 第一局由甲、乙参加而丙轮空,以后每一局由前一局的获胜者与轮空者进行比赛,而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为 ,且各局胜负相互独立.
,且各局胜负相互独立.
求:(I)打满3局比赛还未停止的概率;
(II)比赛停止时已打局数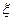 的分别列与期望E
的分别列与期望E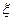 .
.
如图所示,直角梯形ACDE与等腰直角△ABC所在平面互相垂直,F为BC的中点,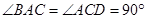 ,AE∥CD,DC=AC=2AE=2.
,AE∥CD,DC=AC=2AE=2.
(Ⅰ)求证:平面B CD
CD 平面ABC
平面ABC
(Ⅱ)求证:AF∥平面BDE;
(Ⅲ)求四面体B-CDE的体积.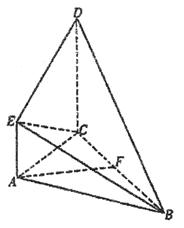
已知函数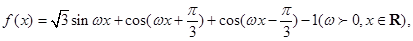 且函数f(x)的最小正周期为
且函数f(x)的最小正周期为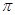 .
.
(1)求函数f(x)的解析式;
(2)在△ABC中,角A,B,C所对的边分别为a,b,c.若f(B)=1,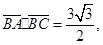 且
且 ,试求
,试求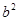 的值.
的值.
已知定义在实数集上的函数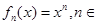 N
N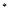 ,其导函数记为
,其导函数记为 ,且满足
,且满足
 ,其中
,其中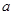 、
、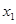 、
、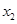 为常数,
为常数,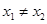 .设函数
.设函数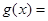
 R且
R且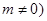 .
.
(Ⅰ)求实数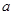 的值;
的值;
(Ⅱ)若函数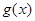 无极值点,其导函数
无极值点,其导函数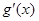 有零点,求m的值;
有零点,求m的值;
(Ⅲ)求函数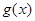 在
在 的图象上任一点处的切线斜率k的最大值
的图象上任一点处的切线斜率k的最大值
如图,椭圆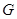 的中心在坐标原点,其中一个焦点为圆
的中心在坐标原点,其中一个焦点为圆 的圆心,右顶点是圆F与x轴的一个交点.已知椭圆
的圆心,右顶点是圆F与x轴的一个交点.已知椭圆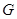 与直线
与直线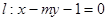 相交于A、B两点.
相交于A、B两点.
(Ⅰ )求
)求 椭圆的方程;
椭圆的方程;
(Ⅱ)求 面积的最大值;
面积的最大值;
某工厂生产一种产品的成本费共由三部分组成:①原材料费每件50元;②职工工资支出7500+20x元;③电力与机器保养等费用为 元.其中x是该厂生产这种产品的总件数.
元.其中x是该厂生产这种产品的总件数.
(Ⅰ)把每件产品的成本费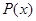 (元)表示成产品件数x的函数,并求每件产品的最低成本费;
(元)表示成产品件数x的函数,并求每件产品的最低成本费;
(Ⅱ)如果该厂生产的这种产品的数量x不超过170件且能全部销售,根据市场 调查
调查 ,每件产品的销售价为
,每件产品的销售价为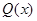 (元),且
(元),且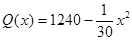 .试问生产多少件产品,总利润最高?并求出最高总利润.(总利
.试问生产多少件产品,总利润最高?并求出最高总利润.(总利 润=总销售额-总的成本)
润=总销售额-总的成本)