某校从参加高一年级期中考试的学生中随机抽取 名学生,将其数学成绩(均为整数)分成六段
名学生,将其数学成绩(均为整数)分成六段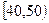 ,
, …
…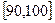 后得到如下部分频率分布直方图.(见下一页图)观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.(见下一页图)观察图形的信息,回答下列问题:
(Ⅰ)求分数在 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的平均分;
(Ⅲ)用分层抽样的方法在分数段为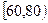 的学生中抽取一个容量为
的学生中抽取一个容量为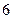 的样本,将该样本看成一个总体,从中任取
的样本,将该样本看成一个总体,从中任取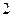 人,求至多有
人,求至多有 人在分数段
人在分数段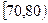 的概率。
的概率。

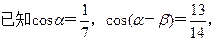

求: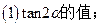
 .
.
某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费每满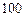 元可以
元可以
转动如图所示的圆盘一次,其中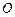 为圆心,且标有
为圆心,且标有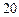 元、
元、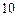 元、
元、 元的三部分区域面积相
元的三部分区域面积相
等. 假定指针停在任一位置都是等可能的.当指针停在某区域时,返相应金额的优惠券.(例
如:某顾客消费了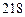 元,第一次转动获得了
元,第一次转动获得了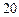 元,第二次获得了
元,第二次获得了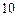 元,则其共获得了
元,则其共获得了
元 优惠券.)顾客甲和乙都到商场进行了消费,并按照规则参与了活动.
优惠券.)顾客甲和乙都到商场进行了消费,并按照规则参与了活动.
⑴若顾客甲消费了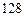 元,求他获得优惠券面额大于
元,求他获得优惠券面额大于 元的概率?
元的概率?
⑵若顾客乙消费了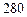 元,求他
元,求他 总共获得优惠券金额不低于
总共获得优惠券金额不低于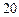 元的概率?
元的概率?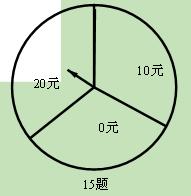
(本小题满分14分)
已知向量 ,
,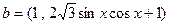 ,函数
,函数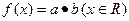 。求:
。求:
(1)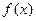 的最小正周期;
的最小正周期;
(2)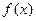 的单调递增区间;
的单调递增区间;
(3)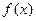 在
在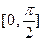 上的最值,并求
上的最值,并求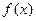 取得最值时对应的
取得最值时对应的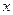 的值。
的值。
(本小题满分12分)一个口袋内装有形状、大小相同的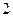 个白球和
个白球和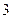 个黑球。
个黑球。
(1)从中随机地摸出一个球不放回,再随机地摸出一个球,求两球同时是黑球的概率;
(2)从中随机地摸出一个球,放回后再随机地摸出一个球,求两球恰好颜色不同的概率;
(本小题满分12分)
已知函数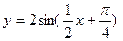 ,
,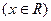 。
。
(1)利用“五点法”画出该函数在长度为一个周期上的简图;
列表:
作图:
(2)说明该函数的图像可由 图像经过怎样的变换得到。
图像经过怎样的变换得到。