品酒师需定期接受酒味鉴别功能测试,一种通常采用的测试方法如下:拿出
瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这
瓶酒,并重新按品质优劣为它们排序,这称为一轮测试。根据一轮 测试中的两次排序的偏离程度的高低为其评为。
测试中的两次排序的偏离程度的高低为其评为。
现设
,分别以
表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令
,则
是对两次排序的偏离程度的一种描述。
(Ⅰ)写出
的可能值集合;
(Ⅱ)假设
等可能地为1,2,3,4的各种排列,求
的分布列;
(Ⅲ)某品酒师在相继进行的三轮测试中,都有
,
(i)试按(Ⅱ)中的结果,计算出现这种现象的概率(假定各轮测试相互独立);
(ii)你认为该品酒师的酒味鉴别功能如何?说明理由。
(本小题满分12分)
现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽调了50人,他们月收入的频数分布及对楼市“楼市限购令”赞成人数如下表.
| 月收入(单位百元) |
[15,25 |
[25,35 |
[35,45 |
[45,55 |
[55,65 |
[65,75 |
| 频数 |
5 |
10 |
15 |
10 |
5 |
5 |
| 赞成人数 |
4 |
8 |
12 |
5 |
2 |
1 |
(Ⅰ)由以上统计数据填下面2乘2列联表并问是否有99%的把握认为“月收入以5500为分界点对“楼市限购令” 的态度有差异;
| 月收入不低于55百元的人数 |
月收入低于55百元的人数 |
合计 |
|
| 赞成 |
 |
 |
|
| 不赞成 |
 |
 |
|
| 合计 |
(Ⅱ)若对在[15,25) ,[25,35)的被调查中各随机选取两人进行追踪调查,记选中的4人中不赞成“楼市限购令”人数为  ,求随机变量
,求随机变量 的分布列及数学期望.
的分布列及数学期望.
(本小题满分12分)
设函数 (
( )的图象过点
)的图象过点 .
.
(Ⅰ)求 的解析式;(Ⅱ)已知
的解析式;(Ⅱ)已知 ,
, ,求
,求 的值.
的值.
已知函数
(Ⅰ)若 在
在 处取得极值,求
处取得极值,求 的值;
的值;
(Ⅱ)讨论 的单调性;
的单调性;
(Ⅲ)证明: 为自然对数的底数)
为自然对数的底数)
已知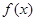 是二次函数,不等式
是二次函数,不等式 的解集是
的解集是 且
且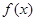 在区间
在区间 上的最大值是12.
上的最大值是12.
(Ⅰ)求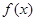 的解析式;
的解析式;
(Ⅱ)是否存在自然数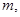 使得方程
使得方程 在区间
在区间 内有且只有两个不等的实数根?若存在,求出
内有且只有两个不等的实数根?若存在,求出 的集合;若不存在,说明理由.
的集合;若不存在,说明理由.
首届世界低碳经济大会在南昌召开,本届大会以“节能减排,绿色生态”为主题.某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本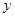 (元)与月处理量
(元)与月处理量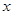 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为: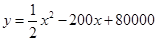 ,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
(Ⅰ)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(Ⅱ)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?