如图,已知椭圆
的离心率为
,以该椭圆上的点和椭圆的左、右焦点
为顶点的三角形的周长为
.一等轴双曲线的顶点是该椭圆的焦点,设
为该双曲线上异于顶点的任一点,直线
和
与椭圆的交点分别为
和
.
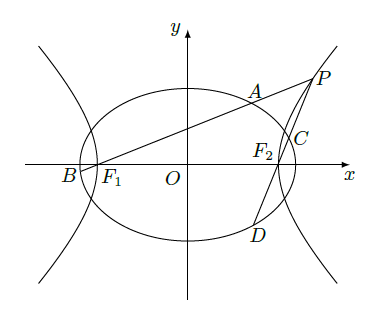
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线
、
的斜率分别为
、
,证明
;
(Ⅲ)是否存在常数
,使得
恒成立?若存在,求
的值;若不存在,请说明理由.
(本小题满分12分) 已知四棱锥 底面ABCD是矩形,PA⊥平面ABCD, AD=2,AB=1,E.F分别是线段AB.BC的中点,
底面ABCD是矩形,PA⊥平面ABCD, AD=2,AB=1,E.F分别是线段AB.BC的中点,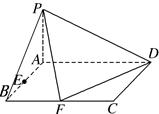
(1)证明:PF⊥FD;
(2)在PA上找一点G,使得EG∥平面PFD;.
(3)若 与平面
与平面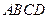 所成的角为
所成的角为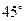 ,求二面角
,求二面角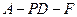 的余弦值.
的余弦值.
(本小题满分12分)
已知全集U = R,非空集合 ,
, .
.
(1)当 时,求(∁U
时,求(∁U )
) ;
;
(2)命题 ,命题
,命题 ,若
,若 是
是 的必要条件,求实数
的必要条件,求实数 的取值范围
的取值范围
(满分14分)数列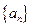 的前
的前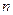 项和为
项和为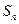 ,
, ,
,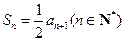 .
.
(1)求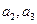 。
。
(2)求数列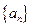 的通项
的通项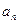 ;
;
(3)求数列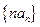 的前
的前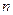 项和
项和
(满分12分)
已知正方体ABCD—A1B1C1D1,其棱长为2,O是底ABCD对角线的交点。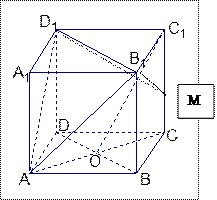
求证:
(1)C1O∥面AB1D1;
(2)A1C⊥面AB1D1。
(3)若M是CC1的中点,求证:平面AB1D1⊥平面MB1D1
(满分12分)已知函数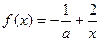 。
。
(1)解关于 的不等式
的不等式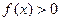 。
。
(2)若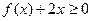 在(0,+∞)上恒成立,求
在(0,+∞)上恒成立,求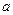 的取值范围
的取值范围