已知函数 , ,
(Ⅰ)若曲线 与曲线 相交,且在交点处有共同的切线,求 的值和该切线方程;
(Ⅱ)设函数 ,当 存在最小值时,求其最小值 的解析式;
(Ⅲ)对(Ⅱ)中的 和任意的 ,证明: .
已知命题p: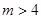 ;命题q:方程
;命题q:方程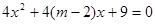 有实根.若
有实根.若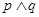 为真,求实数m的取值范围.
为真,求实数m的取值范围.
已知F1、F2分别是椭圆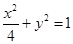 的左、右焦点.
的左、右焦点.
(Ⅰ)若P是第一象限内该图形上的一点,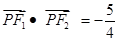 ,求点P的坐标;
,求点P的坐标;
(Ⅱ)设过定点M(0,2)的直线l与椭圆交于同的两点A、B,且∠AOB为锐角(其中O为作标原点),求直线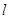 的斜率
的斜率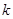 的取值范围.
的取值范围.
)在平面直角坐标系xOy中,点P(a,b)(a>b>0)为动点,F1、F2分别为椭圆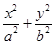 =1的左、右焦点.已知△F1PF2为等腰三角形.
=1的左、右焦点.已知△F1PF2为等腰三角形.
(1)求椭圆的离心率e;
(2)设直线PF2与椭圆相交于A,B两点,M是直线PF2上的点,满足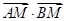 =-2,求点M的轨迹方程.
=-2,求点M的轨迹方程.
如图所示,从双曲线x2-y2=1上一点Q引直线x+y=2的垂线,垂足为N.求线段QN的中点P的轨迹方程.
为了了解小学生的体能情况,抽取了某小学同年级部分学生进行跳绳测试,将所得的数据整理后画出频率分布直方图(如下图),已知图中从左到右的前三个小组的频率分别是0.1,0.3,0.4.第一小组的频数是5.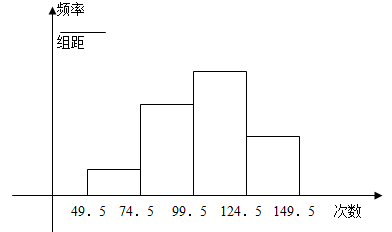
(1)求第四小组的频率和参加这次测试的学生人数;
(2)在这次测试中,学生跳绳次数的中位数落在第几小组内?
(3)参加这次测试跳绳次数在100次以上为优秀,试估计该校此年级跳绳成绩的优秀率是多少?