为了了解小学生的体能情况,抽取了某小学同年级部分学生进行跳绳测试,将所得的数据整理后画出频率分布直方图(如下图),已知图中从左到右的前三个小组的频率分别是0.1,0.3,0.4.第一小组的频数是5.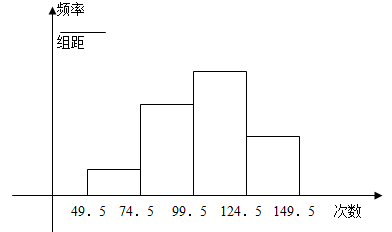
(1)求第四小组的频率和参加这次测试的学生人数;
(2)在这次测试中,学生跳绳次数的中位数落在第几小组内?
(3)参加这次测试跳绳次数在100次以上为优秀,试估计该校此年级跳绳成绩的优秀率是多少?
(本小题满分12分)
在一次海上联合作战演习中, 红方一艘侦察艇发现在北偏东45°方向
红方一艘侦察艇发现在北偏东45°方向 ,相距12n mile的水面上,有蓝方一艘小艇正以每小时10n mile的速度沿南偏东75°方向前进,若侦察艇以每小时14n mile的速度,沿北偏东45°+
,相距12n mile的水面上,有蓝方一艘小艇正以每小时10n mile的速度沿南偏东75°方向前进,若侦察艇以每小时14n mile的速度,沿北偏东45°+ 方向拦截蓝方的小艇,若要在最短的时间内拦截住,求红方侦察艇所需的时间和角
方向拦截蓝方的小艇,若要在最短的时间内拦截住,求红方侦察艇所需的时间和角 的正弦值。
的正弦值。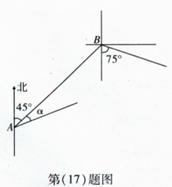
(本小题满分12分)
已知点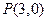 ,点A、B分别在x轴负半轴和y轴上,且
,点A、B分别在x轴负半轴和y轴上,且 ,点
,点 满足
满足 ,当点B在y轴上移动时,记点C的轨迹为E。
,当点B在y轴上移动时,记点C的轨迹为E。
(1)求曲线E的方程;
(2)过点Q(1,0)且斜率为k的直线 交曲线E于不同的两点M、N,若D(
交曲线E于不同的两点M、N,若D( ,0),且
,0),且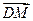 ·
· >0,求k的取值范围。
>0,求k的取值范围。
已知函数
(1)若 在
在 处取得极值,求
处取得极值,求 的单调递增区间;
的单调递增区间;
(2)若 在区间
在区间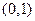 内有极大值和极小值,求实数
内有极大值和极小值,求实数 的取值范围.
的取值范围.
(本小题满分12分)
设椭圆中心在坐标原点,焦点在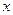 轴上,一个顶点坐标为
轴上,一个顶点坐标为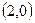 ,离心率为
,离心率为 .
.
(1)求这个椭圆的方程;
(2)若这个椭圆左焦点为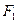 ,右焦点为
,右焦点为 ,过
,过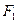 且斜率为1的直线交椭圆
且斜率为1的直线交椭圆 于
于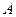 、
、 两点,求
两点,求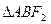 的面积.
的面积.
(本小题满分12分)
某初级中学共有学生2000名,各年级男、女生人数如下表:
| 初一年级 |
初二年级 |
初三年级 |
|
| 女生 |
373 |
x |
y |
| 男生 |
377 |
370 |
z |
如果在全校学生中随机抽取1名学生,抽到初二年级女生的概率是0.19。
(1)求x的值;
(2)现用分层抽样的方法在全校学生中抽取48名学生,问应在初三年级抽取多少名?
(3)已知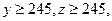 求初三年级中女生比男生多的概率。
求初三年级中女生比男生多的概率。