某超市为了解顾客的购物量及结算时间等信息，安排一名员工随机收集了在该超市购物的50位顾客的相关数据，如下表所示：
一次购物量 （件） |
1≤n≤3 |
4≤n≤6 |
7≤n≤9 |
10≤n≤12 |
n≥13 |
| 顾客数（人） |
 |
20 |
10 |
5 |
 |
| 结算时间（分钟/人） |
0.5 |
1 |
1.5 |
2 |
2.5 |
已知这50位顾客中一次购物量少于10件的顾客占80％.
（1）确定与的值；
（2）若将频率视为概率，求顾客一次购物的结算时间
的分布列与数学期望；
（3）在（2）的条件下，若某顾客到达收银台时前面恰有2位顾客需结算，且各顾客的结算相互独立，求该顾客结算前的等候时间不超过2分钟的概率.
已知从“神州”飞船带回的某种植物种子每粒成功发芽的概率都为
，某植物研究所进行该种子的发芽实验，每次实验种一粒种子，每次实验结果相互独立，假定某次实验种子发芽则称该次实验是成功的，如果种子没有发芽，则称该次实验是失败.若该研究所共进行四次实验，设ξ表示四次实验结束时实验成功的次数与失败的次数之差的绝对值.
（1）求随机变量ξ的数学期望E(ξ)；
（2）记“函数f(x)= x2－
x-1在区间（2，3）上有且只有一个零点”为事件A，求事件A发生的概率P（A）．
选修4-5：不等式选讲（本小题满分10分）
设函数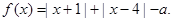
（1）当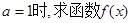
的最小值；
（2）若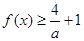
对任意的实数
恒成立，求实数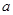
的取值范围.
选修4—4：坐标系与参数方程（本小题满分10分）
已知极坐标系的极点在直角坐标系的原点，极轴与x轴的正半轴重合．曲线C的极坐标方程为
，直线l的参数方程为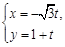
(t为参数，t∈R)．试在曲线C上求一点M，使它到直线l的距离最大．
选修4-2：矩阵与变换（本小题满分10分）
已知矩阵A＝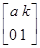
(k≠0)的一个特征向量为α＝
，
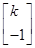A的逆矩阵A－1对应的变换将点(3，1)变为点(1，1)．求实数a，k的值．
选修4-1：几何证明选讲（本小题满分10分）
如下图，AB、CD是圆的两条平行弦，BE//AC，BE交CD于E、交圆于F，过A点的切线交DC的延长线于P，PC=ED=1，PA=2．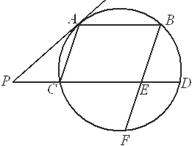
（1）求AC的长；
（2）求证：BE ＝ EF．