选修4—4:坐标系与参数方程(本小题满分10分)
已知极坐标系的极点在直角坐标系的原点,极轴与x轴的正半轴重合.曲线C的极坐标方程为 ,直线l的参数方程为
,直线l的参数方程为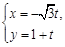 (t为参数,t∈R).试在曲线C上求一点M,使它到直线l的距离最大.
(t为参数,t∈R).试在曲线C上求一点M,使它到直线l的距离最大.
已知函数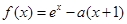 在
在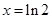 处的切线的斜率为1.
处的切线的斜率为1.
(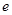 为无理数,
为无理数, )
)
(Ⅰ)求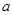 的值及
的值及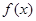 的最小值;
的最小值;
(Ⅱ)当 时,
时,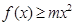 ,求
,求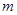 的取值范围;
的取值范围;
(Ⅲ)求证: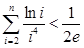
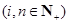 .(参考数据:
.(参考数据: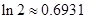 )
)
抛物线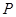 :
: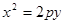 上一点
上一点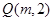 到抛物线
到抛物线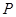 的焦点的距离为
的焦点的距离为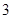 ,
,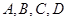 为抛物线的四个不同的点,其中
为抛物线的四个不同的点,其中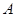 、
、 关于y轴对称,
关于y轴对称,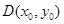 ,
, ,
,  ,
,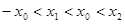 ,直线
,直线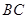 平行于抛物线
平行于抛物线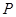 的以
的以 为切点的切线.
为切点的切线.
(Ⅰ)求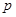 的值;
的值;
(Ⅱ)证明: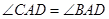 ;
;
(Ⅲ) 到直线
到直线 、
、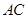 的距离分别为
的距离分别为 、
、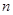 ,且
,且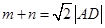 ,
, 的面积为48,求直线
的面积为48,求直线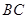 的方程.
的方程.
如图, 为矩形,
为矩形, 为梯形,平面
为梯形,平面
 平面
平面 ,
, ,
, .
.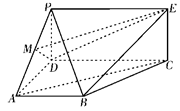
(Ⅰ)若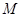 为
为 中点,求证:
中点,求证: ∥平面
∥平面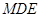 ;
;
(Ⅱ)求平面 与
与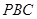 所成锐二面角的大小.
所成锐二面角的大小.
设角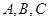 是
是 的三个内角,已知向量
的三个内角,已知向量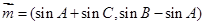 ,
,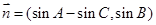 ,且
,且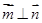 .
.
(Ⅰ)求角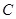 的大小;
的大小;
(Ⅱ)若向量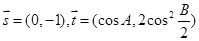 ,试求
,试求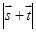 的取值范围.
的取值范围.
已知函数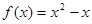 ,
,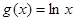 .
.
(Ⅰ)若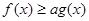 恒成立,求实数
恒成立,求实数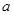 的值;
的值;
(Ⅱ)设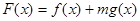 (
(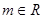
 )有两个极值点
)有两个极值点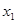 、
、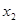 (
(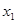
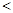
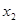 ),求实数
),求实数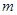 的取值范围,并证明
的取值范围,并证明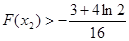 .
.