选修4-1:几何证明选讲(本小题满分10分)
如下图,AB、CD是圆的两条平行弦,BE//AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.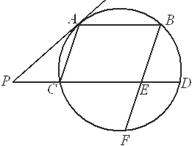
(1)求AC的长;
(2)求证:BE = EF.
已知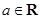 ,函数
,函数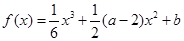 ,
, .
.
(Ⅰ)若曲线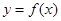 与曲线
与曲线 在它们的交点
在它们的交点 处的切线互相垂直,求
处的切线互相垂直,求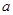 ,
,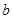 的值;
的值;
(Ⅱ)设 ,若对任意的
,若对任意的 ,且
,且 ,都有
,都有 ,求
,求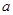 的取值范围.
的取值范围.
如图,在三棱锥 中,
中, ,
, ,
, °,平面
°,平面 平面
平面 ,
, ,
, 分别为
分别为 ,
, 中点.
中点.
(1)求证: ∥平面
∥平面 ;
;
(2)求证: ;
;
(3)求三棱锥 的体积.
的体积.
汽车的碳排放量比较大,某地规定,从2014年开始,将对二氧化碳排放量超过130g/km的轻型汽车进行惩罚性征税.检测单位对甲、乙两品牌轻型汽车各抽取5辆进行二氧化碳排放量检测,记录如下(单位:g/km).
经测算得乙品牌轻型汽车二氧化碳排放量的平均值为 .
.
(1)从被检测的5辆甲品牌轻型汽车中任取2辆,则至少有一辆二氧化碳排放量超过 的概率是多少?
的概率是多少?
(2)求表中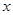 的值,并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性.
的值,并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性.
已知函数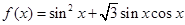 .
.
(1)求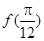 的值;
的值;
(2)当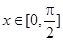 时,求函数
时,求函数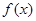 的最大值和最小值.
的最大值和最小值.
设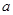 是一个自然数,
是一个自然数,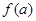 是
是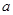 的各位数字的平方和,定义数列
的各位数字的平方和,定义数列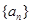 :
: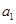 是自然数,
是自然数,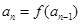 (
(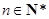 ,
,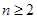 ).
).
(1)求 ,
, ;
;
(2)若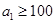 ,求证:
,求证: ;
;
(3)当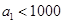 时,求证:存在
时,求证:存在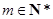 ,使得
,使得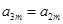 .
.