已知数列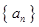 是各项均不为0的等差数列,公差为
是各项均不为0的等差数列,公差为 ,
, 为其前n项和,且满足
为其前n项和,且满足 ,
, .数列
.数列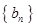 满足
满足 ,
, ,
, 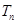 为数列
为数列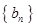 的前
的前 项和.
项和.
(1)求数列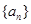 的通项公式
的通项公式 ;
;
(2)若对任意的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数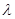 的取值范围;
的取值范围;
(3)是否存在正整数 ,使得
,使得 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有
的值;若不存在,请说明理由.
(本小题满分12分)设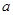 和
和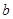 分别是先后抛掷一枚骰子得到的点数,用随机变量
分别是先后抛掷一枚骰子得到的点数,用随机变量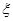 表示函数
表示函数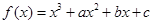 的极值点的个数.
的极值点的个数.
(Ⅰ)求函数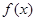 有极值的概率;
有极值的概率;
(Ⅱ)求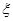 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)求在先后两次出现的点数中有5的条件下,函数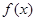 有极值的概率.
有极值的概率.
(本小题满分12分) 若数列 是等比数列,
是等比数列,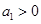 ,公比
,公比 ,已知
,已知 和
和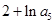 的等差中项为
的等差中项为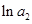 ,且
,且 .
.
(Ⅰ)求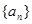 的通项公式;
的通项公式;
(Ⅱ)设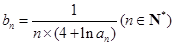 ,求数列
,求数列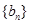 的前
的前 项和.
项和.
(本小题满分12分)在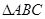 中,
中,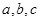 分别是角A、B、C的对边,
分别是角A、B、C的对边,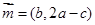 ,
,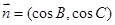 ,且
,且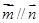 .
.
(Ⅰ)求角B的大小;
(Ⅱ)设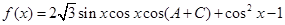 ,
,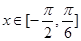 .求函数
.求函数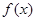 的最值.
的最值.
(本小题满分14分)已知椭圆 ,其中
,其中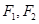 为左、右焦点,O为坐标原点.直线l与椭圆交于
为左、右焦点,O为坐标原点.直线l与椭圆交于 两个不同点.当直线l过椭圆C右焦点F2且倾斜角为
两个不同点.当直线l过椭圆C右焦点F2且倾斜角为 时,原点O到直线l的距离为
时,原点O到直线l的距离为 .又椭圆上的点到焦点F2的最近距离为
.又椭圆上的点到焦点F2的最近距离为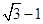 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)以OP,OQ为邻边做平行四边形OQNP,当平行四边形OQNP面积为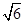 时,求平行四边形OQNP的对角线之积
时,求平行四边形OQNP的对角线之积 的最大值;
的最大值;
(Ⅲ)若抛物线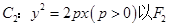 为焦点,在抛物线C2上任取一点S(S不是原点O),以OS为直径作圆,交抛物线C2于另一点R,求该圆面积最小时点S的坐标.
为焦点,在抛物线C2上任取一点S(S不是原点O),以OS为直径作圆,交抛物线C2于另一点R,求该圆面积最小时点S的坐标.
(本小题满分13分) 已知函数 ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(Ⅰ)求曲线 在点
在点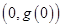 处的切线方程;
处的切线方程;
(Ⅱ)若对任意 ,不等式
,不等式 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(Ⅲ)试探究当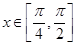 时,方程
时,方程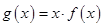 的解的个数,并说明理由.
的解的个数,并说明理由.