如图,四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=900
(1)求证:PC⊥BC
(2)求点A到平面PBC的距离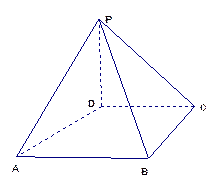
已知直线l经过点P(-2,5),且斜率为
(1)求直线l的方程;
(2)求与直线l切于点(2,2),圆心在直线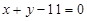 上的圆的方程.
上的圆的方程.
已知在⊿ABC中,A(3,2)、B(-1,5),C点在直线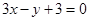 上,若⊿ABC的面积为10,求C点的坐标.
上,若⊿ABC的面积为10,求C点的坐标.
(本小题满分12分)
在直三棱柱ABC—A1B1C1中,∠ABC=90°,BC=CC1,M、N分别为BB1、
A1C1的中点.
(1)求证:CB1⊥平面ABC1;
(2)求证:MN//平面ABC1.
求经过两直线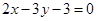 和
和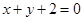 的交点且与直线
的交点且与直线 垂直的直线方程.
垂直的直线方程.
已知函数f(x)=4x3-3x2cosθ+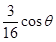 ,其中x∈R,θ为参数,且0≤θ≤2π.
,其中x∈R,θ为参数,且0≤θ≤2π.
(1)当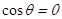 时,判断函数f(x)是否有极值;
时,判断函数f(x)是否有极值;
(2)要使函数f(x)的极小值大于零,求参数θ的取值范围;
(3)若对(2)中所求的取值范围内的任意参数θ,函数f(x)在区间(2A-1,A)内都是增函数,求实数A的取值范围.