如图,正方形 和四边形 所在的平面互相垂直,
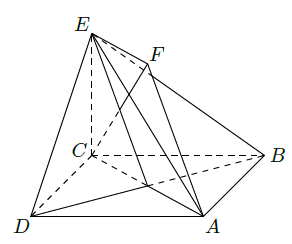
(Ⅰ)求证:
平面
;
(Ⅱ)求证:
平面BDE;
(Ⅲ)求二面角
的大小.
为测量某塔的高度,同学甲先在观察点C测得塔顶A在南偏西 方向上,仰角为
方向上,仰角为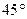 ,然后沿南偏东
,然后沿南偏东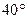 方向前进30米到B点后,测得塔顶A仰角为
方向前进30米到B点后,测得塔顶A仰角为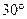 ,试根据同学甲测得的数据计算此塔AD的高度。(其中点A为塔顶,点D为塔顶A在地面上的射影,点B、C、D均在地面上,不考虑同学甲的身高)
,试根据同学甲测得的数据计算此塔AD的高度。(其中点A为塔顶,点D为塔顶A在地面上的射影,点B、C、D均在地面上,不考虑同学甲的身高)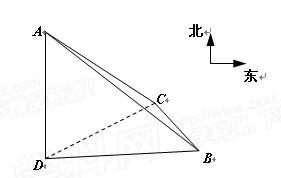
△ABC的三个内角A、B、C的对边的长分别为 a、b、c,有下列两个条件:(1)a、b、c成等差数列;(2)a、b、c成等比数列,现给出三个结论:(1)
a、b、c,有下列两个条件:(1)a、b、c成等差数列;(2)a、b、c成等比数列,现给出三个结论:(1)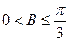 ;(2)
;(2)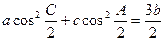 ;(3)
;(3)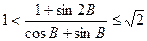 。
。
请你选取给定的两个条件中的一个条件为条件,三个结论中的两个为结论,组建一个你认为正确的命题,并证明之。
(I)组建的命题为:已知_______________________________________________
求证:①_________________ _______
_______ __________________
__________________
②__________________________________________ (II)证明:
(II)证明:
2010年4月14日清晨我国青海省玉树县发生里氏7.1级强震。国家抗 震救灾指挥部迅速成立并调拨一批救灾物资从距离玉树县400千米的某地A运往玉树县,这批救灾物资随17辆车以
震救灾指挥部迅速成立并调拨一批救灾物资从距离玉树县400千米的某地A运往玉树县,这批救灾物资随17辆车以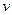 千米/小时的速度匀速直达灾区,为了安全起见,每两辆车之间的间距不得小于
千米/小时的速度匀速直达灾区,为了安全起见,每两辆车之间的间距不得小于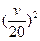 千米。设这批救灾物资全部运送到灾区(不考虑车辆的长度)所需要的时间为
千米。设这批救灾物资全部运送到灾区(不考虑车辆的长度)所需要的时间为 小时。求这批救灾物资全部运送到灾区所需要的最短时间,并指出此时车辆行驶的速度。
小时。求这批救灾物资全部运送到灾区所需要的最短时间,并指出此时车辆行驶的速度。
如图,在四边形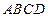 中,
中, ,
, ,
, ,
, ,
,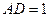 ,求四边形
,求四边形 绕
绕 旋转一周所成几何体的表面积及体积。
旋转一周所成几何体的表面积及体积。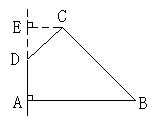
已知 为等比数列,
为等比数列, ,求
,求 的通项公式
的通项公式 。
。