如图,在长方体 中, 分别是棱 上的点, .
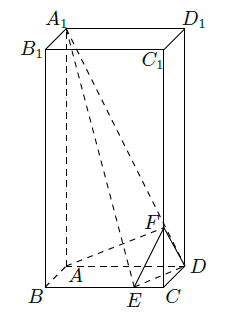
(1)求异面直线
与
所成角的余弦值;
(2)证明
平面
;
(3)求二面角 的正弦值.
某连锁分店销售某种商品,每件商品的成本为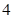 元,并且每件商品需向总店交
元,并且每件商品需向总店交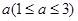 元的管理费,预计当每件商品的售价为
元的管理费,预计当每件商品的售价为 元时,一年的销售量为
元时,一年的销售量为 万件.
万件.
(Ⅰ)求该连锁分店一年的利润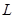 (万元)与每件商品的售价
(万元)与每件商品的售价 的函数关系式
的函数关系式 ;
;
(Ⅱ)当每件商品的售价为多少元时,该连锁分店一年的利润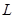 最大,并求出
最大,并求出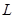 的最大值.
的最大值.
已知函数 .
.
(Ⅰ)若函数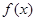 的值域为
的值域为 .求关于
.求关于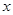 的不等式
的不等式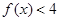 的解集;
的解集;
(Ⅱ)当 时,
时, 为常数,且
为常数,且 ,
,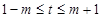 ,求
,求 的最小值.
的最小值.
在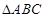 中,角
中,角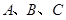 对边分别是
对边分别是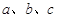 ,且满足
,且满足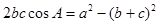 .
.
(Ⅰ)求角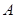 的大小;
的大小;
(Ⅱ)若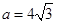 ,
,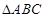 的面积为
的面积为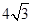 ;求
;求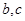 .
.
已知等比数列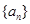 为递增数列,且
为递增数列,且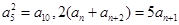 ,
,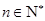 .
.
(Ⅰ)求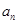 ;
;
(Ⅱ)令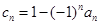 ,不等式
,不等式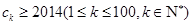 的解集为
的解集为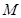 ,求所有
,求所有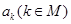 的和.
的和.
已知函数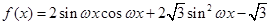 (
(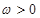 )的最小正周期为
)的最小正周期为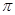 .
.
(Ⅰ)求函数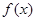 的单调增区间;
的单调增区间;
(Ⅱ)将函数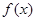 的图象向左平移
的图象向左平移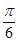 个单位,再向上平移
个单位,再向上平移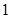 个单位,得到函数
个单位,得到函数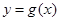 的图象.求
的图象.求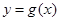 在区间
在区间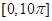 上零点的个数.
上零点的个数.