在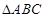 中,角
中,角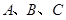 对边分别是
对边分别是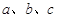 ,且满足
,且满足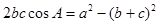 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若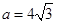 ,
, 的面积为
的面积为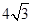 ;求
;求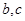 .
.
(本小题满分13分)
已知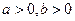 且
且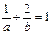 ,求:
,求:
(1)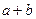 的最小值;
的最小值;
(2)若直线 与
与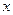 轴、
轴、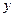 轴分别交于
轴分别交于 、
、 ,求
,求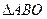 (O为坐标原点)面积的最小值.
(O为坐标原点)面积的最小值.
(本小题满分14分)设函数f(x) =" x2" + bln(x+1),
(1)若对定义域的任意x,都有f(x)≥f(1)成立,求实数b的值;
(2)若函数f(x)在定义域上是单调函数,求实数b的取值范围;
(3)若b = -1,,证明对任意的正整数n,不等式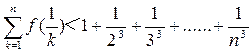 都成立
都成立
(本小题满分13分)椭圆C的中心为坐标原点O,焦点在y轴上,离心率e = ,椭圆上的点到焦点的最短距离为1-e, 直线l与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且 .
.
(1)求椭圆方程;
(2)若 ,求m的取值范围.
,求m的取值范围.
(本小题满分12分)正方体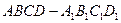 的棱长为
的棱长为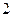 ,
,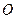 是
是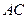 与
与 的交点,
的交点,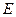 是
是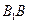 上一点,且
上一点,且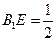 .
.
(1)求证: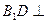 平面
平面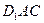 ; (2)求异面直线
; (2)求异面直线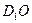 与
与 所成角的余弦值;
所成角的余弦值;
(3)求直线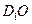 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(本小题满分12分)如图所示是某水产养殖场的养殖大网箱的平面图,四周的实线为网衣,为避免混养,用筛网(图中虚线)把大网箱隔成大小一样的小网箱。
(1)若大网箱的面积为108平方米,每个小网箱的长x,宽y设计为多少米时,才能使围成的网箱中筛网总长度最小;
(2)若大网箱的面积为160平方米,网衣的造价为112元/米,筛网的造价为96元/米,且大网箱的长与宽都不超过15米,则小网箱的长、宽为多少米量,可使总造价最低?