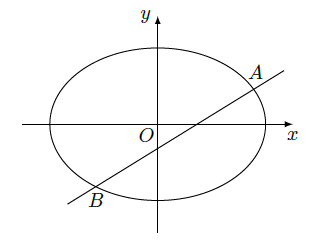
已知m<1，直线l:xmym220，椭圆C:x2m2y21，-优题课

题文

已知 $m > 1$ ，直线 $l : x - m y - \frac{m^{2}}{2} = 0$ ，椭圆 $C : \frac{x^{2}}{m^{2}} + y^{2} = 1$ ， $F_{1} F_{2}$ 分别为椭圆 $C$ 的左、右焦点.
（Ⅰ）当直线 $l$ 过右焦点 $F_{2}$ 时，求直线 $l$ 的方程；
（Ⅱ）设直线 $l$ 与椭圆 $C$ 交于 $A, B$ 两点， $△ A F_{1} F_{2}$ ， $△ B F_{1} F_{2}$ 的重心分别为 $G, H$ .若原点 $O$ 在以线段 $G H$ 为直径的圆内，求实数 $m$ 的取值范围.

科目数学题型解答题难度中等

登录免费查看答案和解析

相关试题

火车有某公司待运的甲种货物1530 t，乙种货物1150 t．现计划用、两种型号的车厢共50节运送这批货物．已知35 t甲种货物和15 t乙种货物可装满一节型货厢；25 t甲种货物和35 t乙种货物可装满一节型货物，据此安排、两种货厢的节数，共有几种方案？若每节型货厢的运费是0.5万元，每节型货物的运费是0.8万元，哪种方案的运费最少？