设F1,F2分别是椭圆E:x2y2b21(0<b<1)的左、-优题课

题文

设 $F_{1}, F_{2}$ 分别是椭圆 $E : x^{2} + \frac{y^{2}}{b^{2}} = 1 (0 < b < 1)$ 的左、右焦点，过 $F_{1}$ 的直线 $l$ 与 $E$ 相交于 $A, B$ 两点，且 $|A F_{1}|, |A B|, |B F_{2}|$ 成等差数列.

（Ⅰ）求 $|A B|$ .

（Ⅱ）若直线 $l$ 的斜率为1，求 $b$ 的值.

科目数学题型解答题难度中等

登录免费查看答案和解析

相关试题

甲盒中有一个红色球，两个白色球，这3个球除颜色外完全相同，有放回地连续抽取2个，每次从中任意地取出1个球，用列表的方法列出所有可能结果，计算下列事件的概率。
（1）取出的2个球都是白球；（2）取出的2个球中至少有1个白球.

已知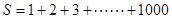，设计算法流程图，输出。

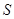计算法流程图，要求输入自变量的值，输出函数的值，并用复合if语句描述算法。

有一个容量为100的样本，数据的分组及各组的频数如下：
（1）列出样本的频率分布表；（2）画出频率分布直方图和频率折线图。

（本小题满分10分）选修4－4 ：坐标系与参数方程
在直角坐标系xOy中，以O为极点，x正半轴为极轴建立极坐标系，曲线C的极坐标方程为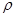
cos（）=1，M,N分别为C与x轴，y轴的交点。
（1）写出C的直角坐标方程，并求M,N的极坐标；
（2）设MN的中点为P，求直线OP的极坐标方程。

试卷网试题网古诗词网作文网范文网