为了考察冰川的融化状况,一支科考队在某冰川山上相距8
的
两点各建一个考察基地,视冰川面为平面形,以过
两点的直线为
轴,线段
的垂直平分线为
轴建立平面直角坐标系(如图)。考察范围到
两点的距离之和不超过10
的区域.
(I)求考察区域边界曲线的方程:
(II)如图4所示,设线段
是冰川的部分边界线(不考虑其他边界),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2
,以后每年移动的距离为前一年的2倍。问:经过多长时间,点A恰好在冰川边界线上?

“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取 名路人进行了问卷调查,得到了如下列联表:
名路人进行了问卷调查,得到了如下列联表:
| 男性 |
女性 |
合计 |
|
| 反感 |
 |
||
| 不反感 |
 |
||
| 合计 |
 |
已知在这 人中随机抽取
人中随机抽取 人抽到反感“中国式过马路”的路人的概率是
人抽到反感“中国式过马路”的路人的概率是
(1)请将上面的列联表补充完整(在答题卷上直接填写结果,不需要写求解过程);
(2)据此资料判断是否有 的把握认为反感“中国式过马路”与性别有关?
的把握认为反感“中国式过马路”与性别有关?
已知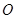 为
为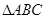 的外心,以线段
的外心,以线段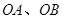 为邻边作平行四边形,第四个顶点为
为邻边作平行四边形,第四个顶点为 ,再以
,再以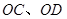 为邻边作平行四边形,它的第四个顶点为
为邻边作平行四边形,它的第四个顶点为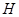 .
.
(1)若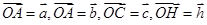 ,试用
,试用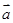 、
、 、
、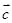 表示
表示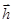 ;
;
(2)证明: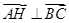 ;
;
(3)若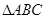 的
的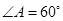 ,
,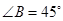 ,外接圆的半径为
,外接圆的半径为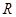 ,用
,用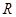 表示
表示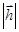 .
.
已知向量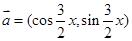 ,
,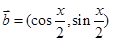 ,且
,且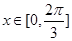 .
.
(1)求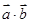 及
及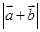 ;
;
(2)若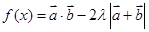 的最小值为
的最小值为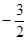 ,求实数
,求实数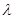 的值.
的值.
已知函数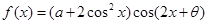 为奇函数,且
为奇函数,且 ,其中
,其中 ,
,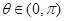 .
.
(1)求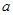 ,
,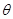 的值;[
的值;[
(2)令 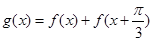 ,
,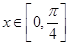 ,求
,求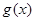 的最值并求出相应的
的最值并求出相应的 的值.
的值.
已知 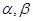 均为锐角,且
均为锐角,且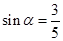 ,
, .
.
(1)求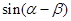 的值;
的值;
(2)求 的值.
的值.