图中左边有一对平行金属板,两板相距为,电压为;两板之间有匀强磁场,磁感应强度大小为,方向平行于板面并垂直于纸面朝里。图中右边有一边长为的正三角形区域(边与金属板垂直),在此区域内及其边界上也有匀强磁场,磁感应强度大小为,方向垂直于纸面朝里。假设一系列电荷量为的正离子沿平行于金属板面、垂直于磁场的方向射入金属板之间,沿同一方向射出金属板之间的区域,并经边中点射入磁场区域。不计重力。

(1)已知这些离子中的离子甲到达磁场边界后,从边界穿出磁场,求离子甲的质量。
(2)已知这些离子中的离子乙从边上的I点(图中未画出)穿出磁场,且长为。求离子乙的质量。
(3)若这些离子中的最轻离子的质量等于离子甲质量的一半,而离子乙的质量是最大的,问磁场边界上什么区域内可能有离子到达。
A、B两辆汽车在笔直的公路上同向行驶.当B车在A车前84 m处时,B车速度为4 m/s,且正以2 m/s2的加速度做匀加速运动,经过一段时间后,B车加速度突然变为零,A车一直以20 m/s的速度做匀速运动,经过12 s后两车相遇.问B车加速行驶的时间是多少?
从斜面上某位置,每隔0.1 s释放一个小球,在连续释放几个后,对在斜面上的小球拍下照片,如图所示,测得sAB ="15" cm,sBC ="20" cm,试求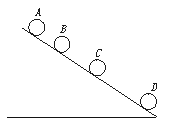
(1)小球的加速度.
(2)拍摄时B球的速度vB=?
(3)拍摄时sCD=?
(4)A球上面滚动的小球还有几个?
一列火车由车站开出做匀加速直线运动时,值班员站在第一节车厢前端的旁边,第一节车厢经过他历时4秒,整列车经过他历时20秒,设各节车厢等长,车厢连接处的长度不计,则:
(1)这列火车共有多少节车厢?
(2)最后九节车厢经过他身边历时多少?
物体在斜坡顶端以1 m/s的初速度和0.5 m/s2的加速度沿斜坡向下作匀加速直线运动,已知斜坡长24米,
求:(1) 物体滑到斜坡底端所用的时间。
(2) 物体到达斜坡中点速度。
(12分)如图18所示,在xOy平面上第Ⅰ象限内有平行于y轴 的有界匀强电场,方向如图所示.y轴上一点P的坐标为(0,y0),有一电子以垂直于y轴的初速度v0从P点垂直射入电场中,当匀强电场的场强为E1时,电子从A点射出,A点坐标为(xA,0),当场强为E2时,电子从B点射出,B点坐标为(xB,0).已知电子的电荷量为e,质量为m,不计电子的重力,E1、E2未知.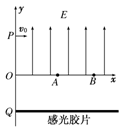
(1)求匀强电场的场强E1、E2之比;
(2)若在第Ⅳ象限过Q点放一张垂直于xOy平面的感光胶片,Q点的坐标为(0,-y0),
求感光胶片上曝光点的横坐标xA′、xB′之比.