以一年为一个周期调查某商品出厂价格及该商品在商店的销售价格时发现:该商品的出厂价格是在6元基础上按月份随正弦曲线波动的,已知3月份出厂价格最高为8元,7月份出厂价格最低为4元,而该商品在商店的销售价格是在8元基础上按月随正弦曲线波动的,并已知5月份销售价最高为10元,9月份销售价最低为6元,假设某商店每月购进这种商品m件,且当月售完,请分别写出该商品的出厂价格函数、销售价格函数、盈利函数的解析式
(本小题满分15分)
如图,已知四棱锥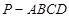 中,平面
中,平面 平面
平面 ,平面
,平面 平面
平面 ,
, 为
为 上任意一点,
上任意一点,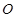 为菱形
为菱形 对角线的交点.
对角线的交点.
(Ⅰ)证明:平面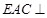 平面
平面 ;
;
(Ⅱ)若 ,三棱锥
,三棱锥 的体积是四棱锥
的体积是四棱锥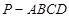 的体积的
的体积的 ,二面角
,二面角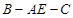 的大小为
的大小为 ,求
,求

(本小题满分14分)
在直角坐标系 中,以
中,以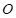 为极点,
为极点, 轴的正半轴为极轴建立极坐标系.己知圆
轴的正半轴为极轴建立极坐标系.己知圆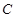 的圆心的
的圆心的
极坐标为 半径为
半径为 ,直线
,直线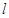 的参数方程为
的参数方程为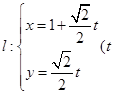 为参数)
为参数)
(Ⅰ)求圆C的极坐标方程;直线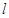 的普通方程;
的普通方程;
(Ⅱ)若圆C和直线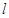 相交于A,B两点,求线段AB的长.
相交于A,B两点,求线段AB的长.
(本小题满分14分)
设 是抛物线
是抛物线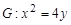 的焦点.
的焦点.
(Ⅰ)过点 作抛物线
作抛物线 的切线,求切线方程;
的切线,求切线方程;
(Ⅱ)设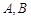 为抛物线
为抛物线 上异于原点的两点,且满足
上异于原点的两点,且满足 ,延长
,延长 分别交抛物线
分别交抛物线 于
于
点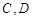 ,求四边形
,求四边形 面积的最小值.
面积的最小值.
(本小题满分14分)
已知条件 :
: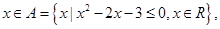
条件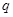 :
: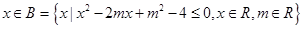
(Ⅰ)若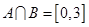 ,求实数
,求实数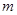 的值;
的值;
(Ⅱ)若 是
是 的充分条件,求实数
的充分条件,求实数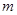 的取值范围.
的取值范围.
已知过点 的动直线
的动直线 与抛物线
与抛物线 相交于
相交于 两点,当直线斜率是
两点,当直线斜率是 时,
时,
(1)求抛物线 的方程;
的方程;
(2)设线段 中垂线在
中垂线在 轴上截距是
轴上截距是 ,求
,求 的取值范围。
的取值范围。